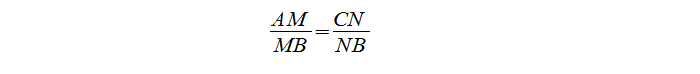Слово Как пишется знак пересекает в геометрии - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Знак пересечения

Определение

Знак пересечения – это символ, указывающий на пересечение прямых, углов, лучей, отрезков, плоскостей и других фигур в геометрии, пересечение множеств в математике (алгебре) и информатике.

Как пишется этот символ пересечения?

Этот знак выглядит и пишется так – ⋂

Его достаточно легко запомнить, он похож на русскую букву «П», начальную букву слова «пересечение».

Как быстро запомнить этот знак?

Просто представьте себе и запомните, что этот символ выглядит как буква «П» и похож на подкову, перевернутую вниз ногами.

Как применяется знак ⋂?

Применяется для обозначения пересечения прямых, углов, лучей, отрезков в геометрии, пересечение множеств в математике (алгебре) и информатике.

Как выглядит знак «не пересечения» в геометрии?

Пример

А ∩ С = ∅ — 2 луча или (2 прямые, 2отрезка) А и С не пересекаются.

Что обозначает знак пересечения наоборот?

Это символ выглядит и пишется следующим образом: ∪

Обозначается термином – «объединение».

Источник

Знаки, обозначающие взаимное расположение объектов

|| – знак параллельности;

≡ – знак совпадения (тождества);

∩– знак пересечения двух геометрических элементов;

= – знак результата геометрического построения;

∟ – знак прямого угла;

Δ – знак треугольника;

∈ – знак принадлежности одного геометрического элемента другому;

A ∈ (ВС) – точка А принадлежит прямой ВС;

С – знак включения, А ∈ Н – прямая А принадлежит плоскости Н;

∩ – знак пересечения, А ∩ Н – прямая А пересекает плоскость Н;

=> – импликация – логическое следствие; означает «если, то …».

ТОЧКА

Метод проекций

В основе правил построения изображений лежит метод проекций. Суть метода заключается в том, что каждой точке трехмерного пространства соответствует определенная точка двухмерного пространства плоскости. Изучение его начинают с построений проекций точки, т. к. любой геометрический объект может рассматриваться как множество точек, заданных по определенному закону. Этот геометрический объект отображается на плоскость по закону проецирования. Процесс отображения называется проецированием. Результатом такого отображения является изображение объекта, которое называется проекцией.

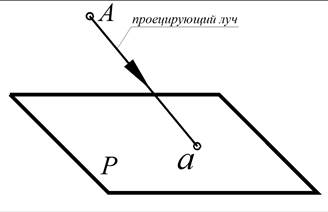
Для построения проекции геометрического объекта задают аппарат проецирования, в который входит объект проецирования,например, точка А,и плоскость проецирования Р (иногда ее называют картинной плоскостью), не проходящая через точку А (рис. 1).Для получения изображения точки А на плоскость Р через нее проводят проецирующий луч до его пересечения с плоскостью Р в точке а. Полученную точку а называют проекцией точки А. Проекция (лат. projectio – выбрасывание вперед).

Рис. 1. Проецирование точки А

Виды проецирования

Задан аппарат проецирования: центр проекций S, плоскость проецирования Р.

В результате центрального проецирования на плоскости Р получится центральная проекция любого геометрического объекта. На рис. 2 показано построение центральной проекции отрезка АВ. Проекционный метод изображения предметов основан на их зрительном представлении. Если соединить все точки предмета прямыми линиями (проекционными лучами) с постоянной точкой S (центр проекции), в которой предполагается глаз наблюдателя, то на пересечении этих лучей с какой-либо плоскостью получается проекция всех точек предмета. Таким образом получаем на плоскости перспективное изображение предмета или центральную проекцию.

Свойства центральных проекций:

– проекция точки – точка;

– проекция прямой – прямая;

– если точка принадлежит прямой, то проекция этой точки принадлежит проекции прямой.

2. Параллельное проецирование – частный случай центрального проецирования, когда центр проецирования бесконечно удален. Поэтому в аппарат проецирования входит: направление проецирования S и плоскость проецирования Р. При этом проецирующие лучи рассматривают как прямые, параллельные между собой и параллельные заданному направлению проецирования S (рис. 3).

Рис. 2. Центральное проецирование отрезка АВ

б

а

Рис. 3. Параллельное проецирование:

а – косоугольное отрезка АВ; б – ортогональное точки А

В зависимости от направления проецирования параллельные проекции могу быть:

– ортогональными (прямоугольными) проекциями – проекционные лучи падают перпендикулярно к картинной плоскости Р (рис. 3б);

– косоугольная проекция – проекционные лучи падают не перпендикулярно к картинной плоскости Р (рис. 3а).

Свойства параллельных проекций:

– проекция точки – точка;

– проекция прямой – прямая;

– если точка принадлежит прямой, то проекция этой точки принадлежит проекции этой же прямой;

– проекции параллельных прямых параллельны;

– отношение отрезков прямой равно отношению их проекций.

Ортогональное проецирование имеет ряд преимуществ перед центральным и косоугольным параллельным проецированием:

– простота построений изображения геометрического объекта;

– точность – сохранение точных форм и размеров проецируемой фигуры на чертеже;

– наглядность –чертеж должен создавать пространственное представление о форме геометрического объекта;

– обратимость – возможностьвосстановления оригинала по проекционным изображениям геометрического объекта.

Источник

Обозначения и символика

Для обозначения геометрических фигур и их проекций, для отображения отношения между ними, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем в курсе используется геометрический язык, составленный из обозначений и символов, принятых в курсе математики (в частности, в новом курсе геометрии в средней школе).

Все многообразие обозначений и символов, а также связи между ними могут быть подразделены на две группы:

группа I — обозначения геометрических фигур и отношений между ними;

группа II обозначения логических операций, составляющие синтаксическую основу геометрического языка.

Ниже приводится полный список математических символов, используемых в данном курсе. Особое внимание уделяется символам, которые применяются для обозначения проекций геометрических фигур.

СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ

А. Обозначение геометрических фигур

1. Геометрическая фигура обозначается — Ф.

2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:

3. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:

Линии уровня обозначаются: h — горизонталь; f— фронталь.

Для прямых используются также следующие обозначения:

(АВ) — прямая, проходящая через точки А а В;

[АВ) — луч с началом в точке А;

[АВ] — отрезок прямой, ограниченный точками А и В.

4. Поверхности обозначаются строчными буквами греческого алфавита:

Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:

α(а || b) — плоскость α определяется параллельными прямыми а и b;

5. Углы обозначаются:

6. Угловая: величина (градусная мера) обозначается знаком , который ставится над углом:

— величина угла АВС;

— величина угла φ.

Прямой угол отмечается квадратом с точкой внутри

7. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — ||.

|АВ| — расстояние между точками А и В (длина отрезка АВ);

|Аа| — расстояние от точки А до линии a;

|Аα| — расстояшие от точки А до поверхности α;

|аb| — расстояние между линиями а и b;

|αβ| расстояние между поверхностями α и β.

π₂ —фрюнтальная плоскость проекций.

При замене плоскостей проекций или введении новых плоскостей последние обозначают π₃, π₄ и т. д.

Постояшную прямую эпюра Монжа обозначают k.

10. Проекции точек, линий, поверхностей, любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса, соответствующего плоскости проекции, на которой они получены:

11. Следы плоскостей (поверхностей) обозначаются теми же буквами, что и горизонталь или фронталь, с добавлением подстрочного индекса _0α, подчеркивающего, что эти линии лежат в плоскости проекции и принадлежат плоскости (поверхности) α.

12. Следы прямых (линий) обозначаются заглавными буквами, с которых начинаются слова, определяющие название (в латинской транскрипции) плоскости проекции, которую пересекает линия, с подстрочным индексом, указывающим принадлежность к линии.

Например: H_a — горизонтальный след прямой (линии) а;

F_a — фронтальный след прямой (линии ) a.

13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами _{1,2,3. n:}

Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом ₀:

14. Аксонометрические проекции точек, линий, поверхностей обозначаются теми же буквами, что и натура с добавлением верхнего индекса 0 :

15. Вторичные проекции обозначаются путем добавления верхнего индекса 1 :

Для облегчения чтения чертежей в учебнике при оформлении иллюстративного материала использованы несколько цветов, каждый из которых имеет определенное смысловое значение: линиями (точками) черного цвета обозначены исходные данные; зеленый цвет использован для линий вспомогательных графических построений; красными линиями (точками) показаны результаты построений или те геометрические элементы, на которые следует обратить особое внимание.

Источник

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

Задача № 1 из учебника Атанасян 7-9 класс

Решение задачи

Опишем взаимное расположение точек и прямой.

Как обозначается пересечение прямых

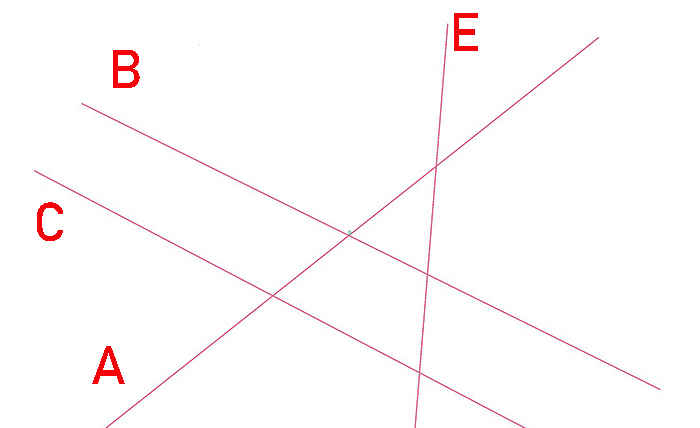
Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Третий случай расположения прямых

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник

В учебниках по геометрии часто встречаются задачи на подобие фигур. Какой знак используется для обозначения подобия фигур? Какие фигуры называются подобными? Поговорим обо всем этом в нашей статье.

Определение и знак подобия в геометрии

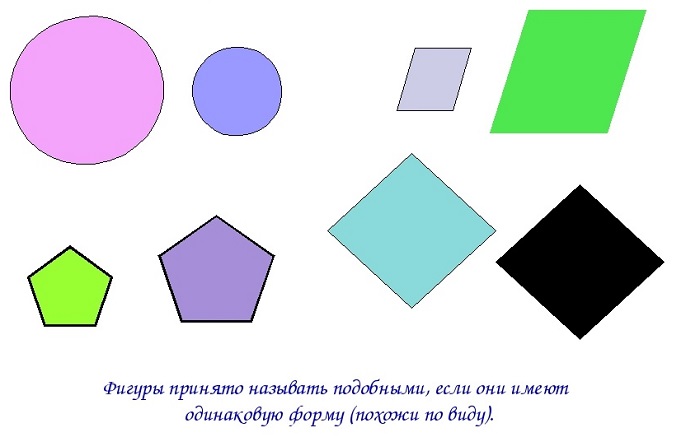
На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.

Для обозначения термина «подобие» в геометрии используют знак «тильда», который является типографским символом и обозначается волнистой чертой:

Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо:

1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.

Коэффициент подобия треугольников и знак подобия

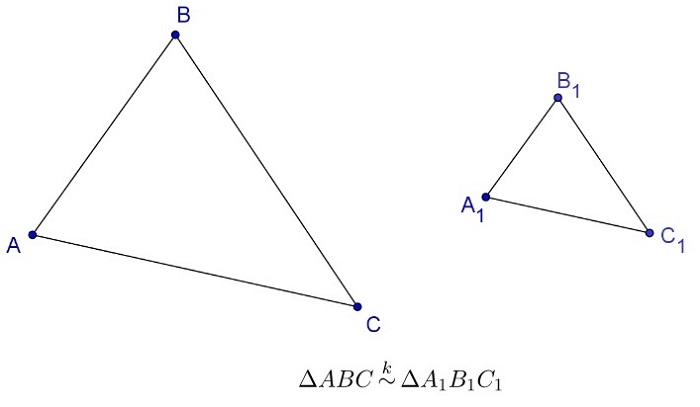
Часто сверху знака подобия выставляют коэффициент подобия треугольников:

В математических задачах и уравнениях «тильду» используют для маркирования разных типов подобия. Часто применяется для обозначения подобия, эквивалентности.

В алгебре высказываний знаком

обозначают логическую операцию «эквиваленция».

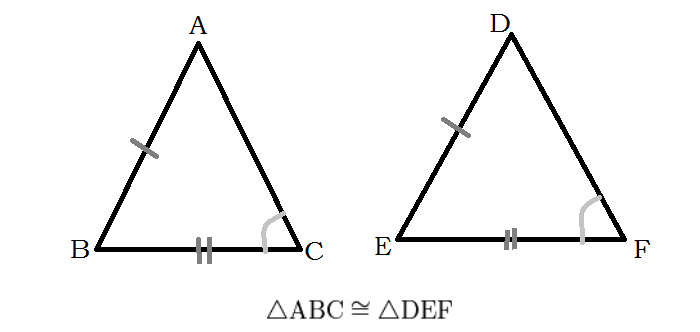
При сочетании тильды и знака равенства получают обозначение отношения конгруэнтности, определения в геометрии, применяемого в контексте обозначения равенства различных фигур и тел (углов, отрезков):

Признаки подобия прямоугольных треугольников

Острые углы: наличие равного острого угла в прямоугольных треугольниках делает их подобными.

Два катета: общая пропорциональность катетам одного прямоугольного треугольника к катетам второго делает их подобными.

Катет и гипотенуза: пропорциональность катета и гипотенузы одного прямоугольного треугольника к катету и гипотенузе второго прямоугольного треугольника делает их подобными.

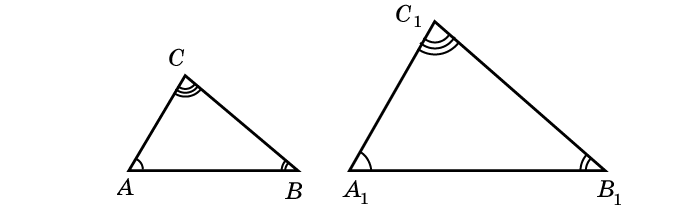
треугольник ∆ABC и треугольник ∆A₁B₁C₁ считаются подобными при равнозначности углов и пропорциональности сторон;

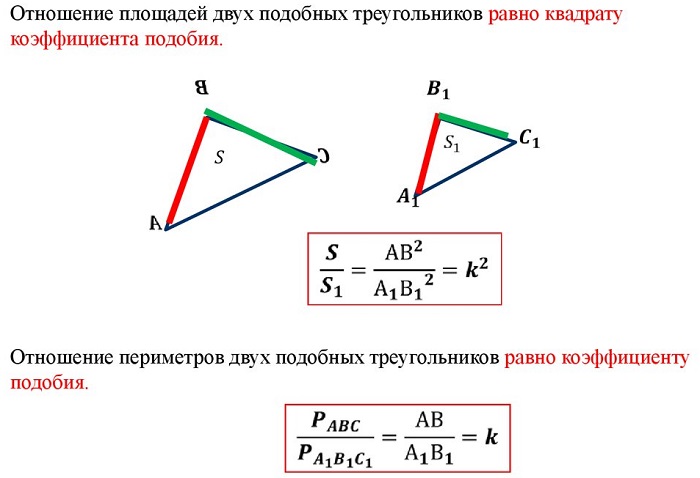
отношение площадей подобных треугольников равно квадрату коэффициента подобия.

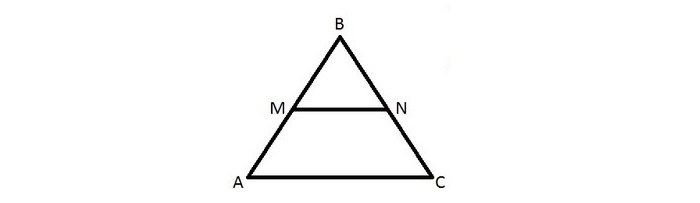
Доказательство подобия треугольников через среднюю линию

Требуется доказательство подобия треугольников ∆MBN и ∆ABC.

Посмотрев на ∆MBN и ∆ABC, видим, что угол В — общий, а отношение:

Отсюда делаем вывод, что ∆MBN

∆ABC по II признаку подобия треугольников, что и требовалось доказать.

Примеры решения задач по геометрии на тему «Подобие треугольников»

Источник