Параллельность прямых
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение параллельности прямых
Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.
Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.
Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.
Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.
На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Свойства и признаки параллельных прямых
Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.
Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.
Если секущая проходит через две параллельные прямые, то:
∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.
∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.

Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.
А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.
Задача 1
Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.
Решение
Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.
Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.
Задача 2
Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.
Решение
Поскольку а II b, значит ∠MKD + ∠KDN = 180°.
Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.
Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.
Параллельные прямые, признаки и условия параллельности прямых
В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.
Параллельные прямые: основные сведения
Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.
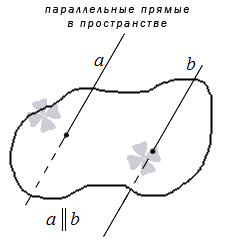
Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.
Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.
Сформулируем утверждение, играющее важную роль в изучаемой теме.
Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.
В случае, когда речь идет о пространстве, верна теорема:
Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.
Параллельность прямых: признаки и условия параллельности
Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых. Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.
В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.
Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.
Перед тем, как дать точную формулировку необходимого и достаточного условия, напомним еще несколько дополнительных понятий.
Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.
Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:
Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.
Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:
В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.
Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.
На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.
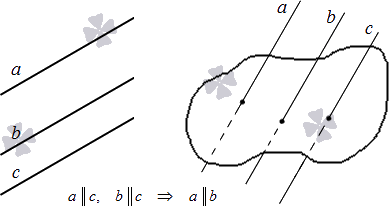
В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.
Доказательство признака изучается в программе геометрии 10 класса.
Дадим иллюстрацию указанных теорем:
Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.
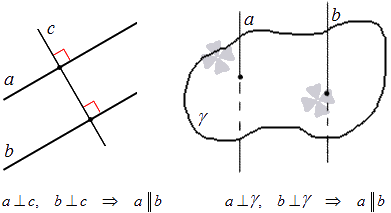
На плоскости две прямые, перпендикулярные третьей, параллельны между собой.
Сформулируем аналогичное для трехмерного пространства.
В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.
Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е., чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т.д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.
Параллельность прямых в прямоугольной системе координат
В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.
Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.
Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.
Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.
A 1 = t · A 2 B 1 = t · B 2
Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.
a x = t · b x a y = t · b y
Решение
Запишем уравнение прямой в отрезках в виде общего уравнения:
Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.
Ответ: заданные прямые не параллельны.
Решение
Мы видим, что уравнения прямых y = 2 x + 1 и y = 2 x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.
Следующим шагом определим выполнение условия параллельности заданных прямых.
Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.
Ответ: данные прямые параллельны.
Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.
Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.
a → = t · b → ⇔ a x = t · b x a y = t · b y a z = t · b z
Решение
Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.
Ответ: параллельность заданных прямых доказана.
Параллельные прямые
Параллельные прямые – подарок судьбы в решении многих задач.
Они дают тебе множество равных углов! И на них основывается много признаков фигур.
Что, безусловно, будет очень полезно.
Читай эту статью – будешь знать о них все!
И получишь заслуженные баллы на ЕГЭ.
Параллельные прямые — коротко о главном
Параллельные прямые – это прямые, которые лежат в одной плоскости и не пересекаются, сколько бы их не продолжали: \( \displaystyle a\parallel b\).
Секущая – прямая, пересекающая две параллельные прямые: \( \displaystyle c\).
Аксиома параллельных прямых: через любую точку плоскости, расположенную вне данной прямой, можно провести единственную прямую, параллельную данной.
\( \displaystyle \angle 4\) и \( \displaystyle \angle 6\), \( \displaystyle \angle 3\) и \( \displaystyle \angle5\) – внутренние накрест лежащие углы;
\( \displaystyle \angle 5\) и \( \displaystyle \angle 4\), \( \displaystyle \angle 6\) и \( \displaystyle \angle 3\) – внутренние односторонние углы;
\( \displaystyle \angle 1\) и \( \displaystyle \angle 8\), \( \displaystyle \angle 2\) и \( \displaystyle \angle 7\) – внешние односторонние углы;
\( \displaystyle \angle 1\) и \( \displaystyle \angle 5\), \( \displaystyle \angle 4\) и \( \displaystyle \angle 8\), \( \displaystyle \angle 2\) и \( \displaystyle \angle 6\), \( \displaystyle \angle 3\) и \( \displaystyle \angle 7\) – соответственные углы.
Свойства параллельных прямых
Если две параллельные прямые пересечены третьей (секущей) прямой, то:
внутренние накрест лежащие углы равны: \( \displaystyle \angle 3=\angle 5\), \( \displaystyle \angle 4=\angle 6\);
соответственные углы равны: \( \displaystyle \angle 1=\angle 5\), \( \displaystyle \angle 4=\angle 8\), \( \displaystyle \angle 2=\angle 6\), \( \displaystyle \angle 3=\angle 7\);
сумма любых двух внутренних односторонних углов равна \( \displaystyle 180<>^\circ \): \( \displaystyle \angle 3+\angle 6=180<>^\circ \), \( \displaystyle \angle 4+\angle 5=180<>^\circ \);
сумма любых двух внешних односторонних углов равна \( \displaystyle 180<>^\circ \): \( \displaystyle \angle 1+\angle 8=180<>^\circ \), \( \displaystyle \angle 2+\angle 7=180<>^\circ \).
Признаки параллельных прямых
Определение параллельных прямых
Прямые называются параллельными, если они лежат в одной плоскости и не пересекаются, сколько бы их не продолжали.
Принято обозначение:
\( \displaystyle a//b\) – читается как \( \displaystyle a\) параллельна \( \displaystyle b\).
Самым важным фактом, который нужно принять без доказательства (не только тебе, но и любому математику) для того, чтобы вся геометрия не развалилась и не превратилась в какую-то неузнаваемую теорию, является так называемая «аксиома параллельных прямых».
Часто ее еще называют «пятый постулат Евклида». Формулируем:
Аксиома параллельных прямых или пятый постулат Евклида
Через любую точку плоскости, расположенную вне данной прямой, можно провести единственную прямую, параллельную данной.
Смотри: через любую точку \( \displaystyle A\) проходит только одна прямая \( \displaystyle b\), которая параллельна \( \displaystyle a\), все остальные будут пересекать прямую \( \displaystyle a\).
Казалось бы: чего проще – ну, одна так одна…
Но ты себе просто не представляешь, сколько споров вели математики на протяжении прямо-таки тысячелетий, прежде чем осознали истинную роль этой аксиомы о параллельных прямых.
В конце концов, уже в 19-м веке, после открытий Лобачевского, Гаусса и других ученых стало ясно, что можно построить и другие виды геометрии, в которых не выполняется аксиома параллельных прямых, в которых ее можно выбросить, но эти геометрии уже оказываются не геометриями плоскости, а геометриями на каких-то хитрых поверхностях.
А наша привычная плоскость оттого и называется евклидовой, что при построении геометрии на ней, при решении всех задачек и доказательстве теорем мы считаем этот многострадальный пятый постулат Евклида выполнимым.
Ну вот, а теперь возникает два вопроса:
Ответ на первый вопрос называется «свойства параллельных прямых», а ответ на второй вопрос называется «признаки параллельных прямых».
Но прежде нам понадобится много названий, которые нужно запомнить, как таблицу умножения.
Термины: секущая, внутренние и внешние углы
Итак, ситуация: две прямые пересечены третьей (она называется секущей )
Получается куча углов. Целых \( \displaystyle 8\) штук.
Приняты такие названия этих углов:
\( \displaystyle \angle 4\) и \( \displaystyle \angle 6\) называются внутренними накрест лежащими углами
\( \displaystyle \angle 3\) и \( \displaystyle \angle5\) – тоже внутренние накрест лежащие углы.
Название говорит само за себя: \( \displaystyle \angle 4\) и \( \displaystyle \angle 6\), так же, как и \( \displaystyle \angle 3\) и \( \displaystyle \angle5\) лежат «накрест» — по разные стороны от секущей и «внутри», между прямыми \( \displaystyle a\) и \( \displaystyle b\).
Они лежат с одной стороны от секущей и «внутри» между прямыми \( \displaystyle a\) и \( \displaystyle b\).
\( \displaystyle \angle 1\) и \( \displaystyle \angle 8\) (а еще \( \displaystyle \angle 2\) и \( \displaystyle \angle 7\)) называются внешними односторонними углами (ты уже догадался, почему?)
И последнее название: соответственные углы.
Обрати внимание, \( \displaystyle \angle 1\) и \( \displaystyle \angle 5\) лежат в одинаковых «соответственных» местах около точек \( \displaystyle A\) и \( \displaystyle B\). То же можно сказать и об остальных перечисленных парах – посмотри на рисунок.
Свойства параллельных прямых
Напоминаем (а то отвлеклись на названия), что пытаемся ответить на вопрос: если \( \displaystyle a//b\), то что?
Если две параллельные прямые пересечены третьей (секущей) прямой, то:
Запомни – все задачи с участием слова «параллельность» решаются с помощью этой теоремы о свойствах параллельных прямых.
А теперь, наоборот, признаки параллельных прямых.
Признаки параллельных прямых
То есть, как бы узнать, что прямые параллельны?
Если две прямые (\( \displaystyle a\) и \( \displaystyle b\)) пересечены третьей и оказалось, что:
то прямые \( \displaystyle a\) и \( \displaystyle b\) – параллельны
Параллельные прямые
Параллельные прямые
Содержание
В Евклидовой геометрии
Параллельными (иногда — равнобежными) прямыми называются прямые, которые лежат в одной плоскости и либо совпадают, либо не пересекаются. В некоторых школьных определениях совпадающие прямые не считаются параллельными, здесь такое определение не рассматривается.
Свойства
В геометрии Лобачевского
В геометрии Лобачевского в плоскости через точку Невозможно разобрать выражение (лексическая ошибка): C вне данной прямой AB
Все остальные прямые, не пересекающие данную, называются ультрапараллельными или расходящимися.
См. также
Полезное
Смотреть что такое «Параллельные прямые» в других словарях:
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ — ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ, непересекающиеся прямые, лежащие в одной плоскости … Современная энциклопедия
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ — непересекающиеся прямые, лежащие в одной плоскости … Большой Энциклопедический словарь
Параллельные прямые — ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ, непересекающиеся прямые, лежащие в одной плоскости. … Иллюстрированный энциклопедический словарь
Параллельные прямые — в евклидовой геометрии, прямые, которые лежат в одной плоскости и не пересекаются. В абсолютной геометрии (См. Абсолютная геометрия) через точку, не лежащую на данной прямой, проходит хотя бы одна прямая, не пересекающая данную. В… … Большая советская энциклопедия
параллельные прямые — непересекающиеся прямые, лежащие в одной плоскости. * * * ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ, непересекающиеся прямые, лежащие в одной плоскости … Энциклопедический словарь
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ — в евклидовой геометрии прямые, к рые лежат в одной плоскости и не пересекаются. В абсолютной геометрии через точку, не лежащую на данной прямой, проходит хотя бы одна прямая, не пересекающая данную. В евклидовой геометрии существует только одна… … Математическая энциклопедия
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ — непересекающиеся прямые, лежащие в одной плоскости … Естествознание. Энциклопедический словарь
Параллельные миры в фантастике — Возможно, эта статья содержит оригинальное исследование. Добавьте ссылки на источники, в противном случае она может быть выставлена на удаление. Дополнительные сведения могут быть на странице обсуждения. У это … Википедия
Параллельные миры — Параллельный мир (в фантастике) реальность, существующая каким то образом одновременно с нашей, но независимо от неё. Эта автономная реальность может иметь различные размеры: от небольшой географической области до целой вселенной. В параллельном … Википедия
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Смотреть что такое «ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ» в других словарях:
Параллельные прямые — Содержание 1 В Евклидовой геометрии 1.1 Свойства 2 В геометрии Лобачевского … Википедия
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ — непересекающиеся прямые, лежащие в одной плоскости … Большой Энциклопедический словарь
Параллельные прямые — ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ, непересекающиеся прямые, лежащие в одной плоскости. … Иллюстрированный энциклопедический словарь
Параллельные прямые — в евклидовой геометрии, прямые, которые лежат в одной плоскости и не пересекаются. В абсолютной геометрии (См. Абсолютная геометрия) через точку, не лежащую на данной прямой, проходит хотя бы одна прямая, не пересекающая данную. В… … Большая советская энциклопедия
параллельные прямые — непересекающиеся прямые, лежащие в одной плоскости. * * * ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ, непересекающиеся прямые, лежащие в одной плоскости … Энциклопедический словарь
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ — в евклидовой геометрии прямые, к рые лежат в одной плоскости и не пересекаются. В абсолютной геометрии через точку, не лежащую на данной прямой, проходит хотя бы одна прямая, не пересекающая данную. В евклидовой геометрии существует только одна… … Математическая энциклопедия
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ — непересекающиеся прямые, лежащие в одной плоскости … Естествознание. Энциклопедический словарь
Параллельные миры в фантастике — Возможно, эта статья содержит оригинальное исследование. Добавьте ссылки на источники, в противном случае она может быть выставлена на удаление. Дополнительные сведения могут быть на странице обсуждения. У это … Википедия
Параллельные миры — Параллельный мир (в фантастике) реальность, существующая каким то образом одновременно с нашей, но независимо от неё. Эта автономная реальность может иметь различные размеры: от небольшой географической области до целой вселенной. В параллельном … Википедия