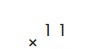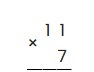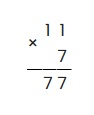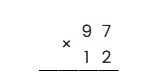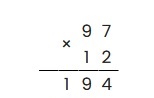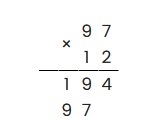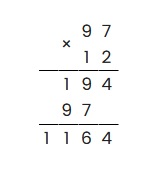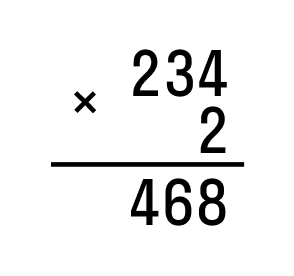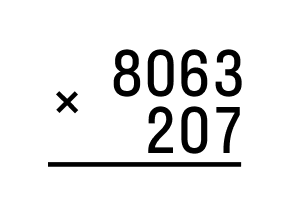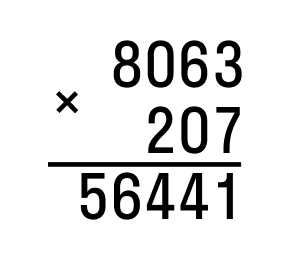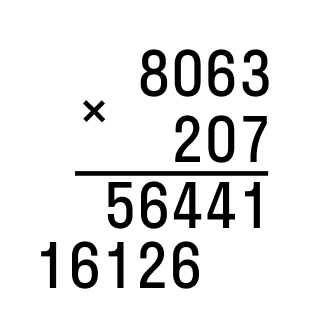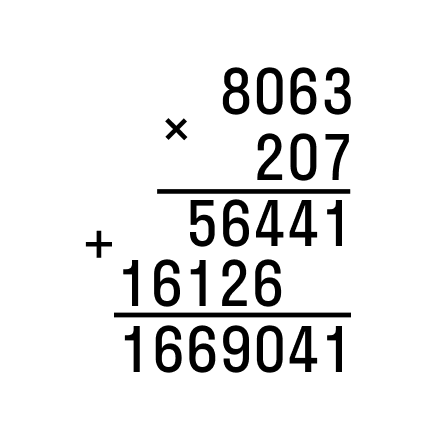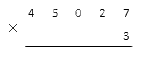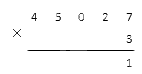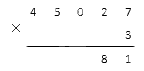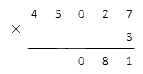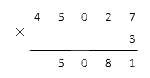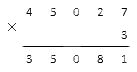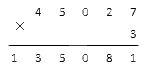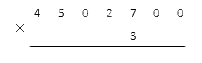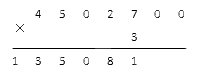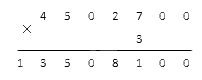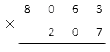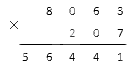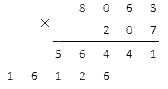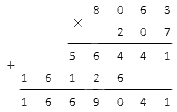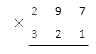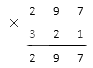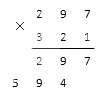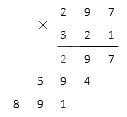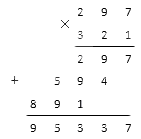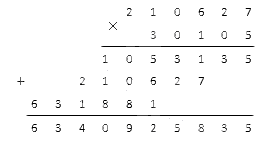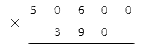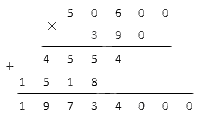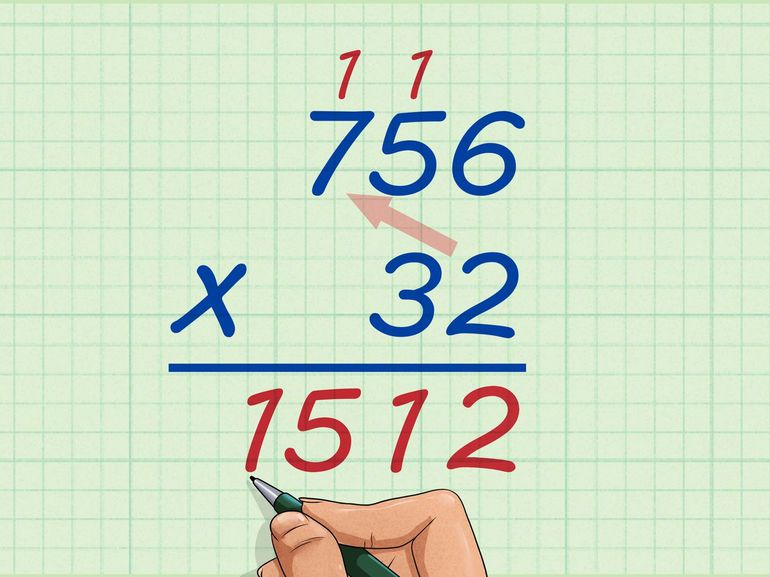Умножение в столбик
Сегодня мы рассмотрим вопрос, касающийся умножению в столбик. Познакомимся с алгоритмом и закрепим материал на конкретных примерах.
Алгоритм умножения в столбик
Для нахождения произведения двух натуральных чисел, воспользуемся следующим правилом:
Примеры
Умножение в столбик двузначного числа на однозначное
Пример: умножить 11 на 7
Выполним умножение исходя из вышеприведенного алгоритма:
Запишем первый множитель и поставим знак умножения:
Запишем ниже второй множитель — 7, соблюдая разрядность и поставим горизонтальную черту, т.е так:
Далее необходимо перемножить каждую цифру второго множителя с каждой цифрой первого. Т.к. во втором множителе всего одна цифра, перемножаем её с с цифрами первого. Получится, что необходимо дважды перемножить 7 с единицей — это и будет ответом. Записываем под чертой.
Умножение в столбик двузначных чисел
Пример: умножить 97 на 12
Аналогично предыдущему примеру, запишем множители, поставим знак умножения, проведем черту:
Перемножим крайнюю правую цифру второго множителя с каждой цифрой первого, таким образом:
Аналогично предыдущему шагу, перемножаем оставшуюся цифру второго множителя (единицу) со всеми цифрами первого (7 и 9). При записи не забываем сдвинуться на разряд влево, т.е:
Последним шагом необходимо сложить получившиеся значения, таким образом:
Умножение в столбик трехзначных и более разрядных чисел производится аналогично!
Как умножать в столбик
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Основные понятия
Во всем мире принято использовать эти десять цифр для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью создается любое натуральное число.
Название числа напрямую зависит от количества знаков.
Разряд — это позиция, на которой стоит цифра в записи. Их принято отсчитывать с конца.
Разряд единиц — то, чем заканчивается любое число. Разряд десятков — то, что находится перед разрядом единиц. Разряд сотен стоит перед разрядом десятков. На место отсутствующего разряда всегда можно поставить ноль.
Умножение — арифметическое действие, в котором участвуют два аргумента — множители. Результат их умножения называется произведением.
Свойства умножения
От перестановки множителей местами произведение не меняется.
Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением.
Самое главное в процессе вычисления — это знание таблицы умножения. Это сделает подсчет упорядоченным и быстрым.
Важно помнить правило: умножение в столбик с нулями дает в результате ноль:
Алгоритм умножения в столбик
Чтобы понять, как умножать в столбик — рассмотрим действия по шагам:
Запишем пример в строку. Выберем и подчеркнем из двух чисел наименьшее, чтобы не забыть при новой записи поставить его вниз.
Записываем произведение в виде столбика. Сначала наибольший множитель, затем наименьший, тот что мы подчеркнули ранее. Слева ставим соответствующий знак и проводим черту под которой будем записывать ход решения. Важно обратить внимание разряды, чтобы единицы стояли стоять под единицами, десятки под десятками и т. д.
Поэтапно производим необходимые действия. Каждую цифру первого множителя нужно умножить на крайнюю цифру второго. Это действие происходит справа налево: единицы, десятки, сотни.
Если результат получится двузначным, под чертой записывается только последняя его цифра. Остальное переносим в следующий разряд путем сложения со значением, полученным при следующем умножении.
После умножения на единицу второго множителя с остальными цифрами необходимо провести аналогичные манипуляции. Результаты записывать под чертой, сдвигаясь влево на одну позицию.
Складываем то, что нашли и получаем ответ.
Умножение на однозначное число
Для решения задачи по произведению двух натуральных чисел, одно из которых однозначное, а другое — многозначное, нужно использовать способ столбика. Для вычисления воспользуемся последовательностью шагов, которую рассмотрели выше.
Возьмем пример 234 × 2:
Запишем первый множитель, а под ним второй. Соответствующие разряды расположены друг под другом. Двойка находится под четверкой.
Последовательно умножаем каждое число в первом множителе на второй, начиная с единиц и продвигаясь к десяткам и сотням.
Ответ запишем под чертой:
Производить действия необходимо в следующей последовательности:
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Умножение двух многозначных чисел
Если оба множителя — многозначные натуральные числа, нужно действовать следующим образом.
Рассмотрим пример 207 × 8063:
Сначала запишем наибольшее 8063, затем наименьшее 207. Нужно разместить цифры друг под другом справа налево:
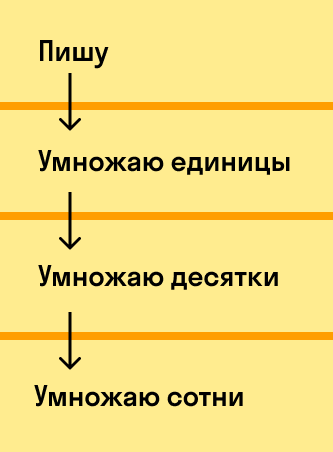
Последовательно перемножаем значения разрядов. Результатом является неполное произведение.
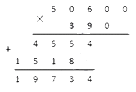
Далее перемножаем десятки. Первый множитель умножим на значение разряда десятков второго и т. д. Результат запишем под чертой.
По аналогии действуем с сотыми. Ноль пропускаем в соответствии с правилом. Так получилось второе неполное произведение:
Далее складываем два произведения в столбик.
Получившееся семизначное число — результат умножения исходных натуральных чисел.
Ответ: 8 063 × 207 = 1 669 041.
Примеры на умножение в столбик
Самостоятельное решение задачек помогает быстрее запомнить правила и натренировать скорость. Не важно, в каком классе учится ребенок — в 1, 3 или 4 — эти примеры подойдут всем.
Умножение в столбик — удобные способы и примеры решения
Перемножение однозначных чисел мало у кого вызывает затруднение, ведь для решения таких примеров существует специальная таблица.
Вычислять же значения дробей и многозначных чисел в строку бывает довольно затруднительно.
удержать промежуточные результаты в голове порой просто невозможно. Как раз для таких случаев придумано умножение в столбик — этот метод значительно упрощает математические вычисления.
Необходимый минимум
Преимущество использования «столбиков» очевидно — пропадает необходимость считать в уме или всегда держать при себе калькулятор. Даже действительно длинные числа с помощью этого метода умножаются без лишних проблем. Достаточно иметь при себе:
Если же с последним пока ещё возникают затруднения, можно положить её рядом с собой и сверять по ходу решения. Правда, при таком раскладе процесс затянется на какое-то время, а полученный результат желательно перепроверить. Ведь одна маленькая ошибка в начале или середине вычисления сделает ответ заведомо неверным.
Регулярное решение примеров столбиком тренирует внимательность и память ребёнка, учит его концентрироваться на отдельно взятой задаче. Это также удобный способ закрепить базовые математические знания.
Как умножать столбиком
Чтобы научиться решать примеры, необходимо понять и отработать базовый алгоритм.
В целом он достаточно прост:
Метод столбиков не подходит для решения примеров, содержащих корни или возведённые в степень числа.
Прежде чем приступить к вычислениям, «проблемные» цифры нужно преобразовать до целых или десятичных.
Решение базовых примеров
Для большей наглядности стоит привести примеры умножения двузначных и трёхзначных чисел.
Пример 1 — отыскать произведение чисел 58 и 23. Решение задания:
По такому же принципу происходит умножение трёхзначных чисел. Разве что вычисление потребует чуть больше времени, а количество промежуточных результатов увеличится.
Пример 2 — решить выражение 659х854. Пошаговое решение:
При затруднениях в процессе решения можно проверить правильность умножения столбиком онлайн-калькулятором. А также существуют специальные генераторы примеров, которые используют как своеобразный тренажёр для закрепления изученного материала.
Целые числа с нулями
В ситуациях с нулями немного сложнее.
Если нолик «потерялся» где-то в середине, то в процессе решения его следует пропустить. Ведь умножение абсолютно любого числа на 0 в итоге даёт этот же 0. Поэтому можно сразу переходить к следующей цифре и заполнить строку под чертой, отступив не на 1, а на 2 единицы.
Что касается таких чисел как 10, 100, 1200, 12030 и т. п. — суть такая же, но алгоритм решения отличается. Вычисления проводят лишь с цифрами, отличными от нуля. А все «0» на конце чисел просто игнорируются. Хотя после сложения их количество надо подсчитать и добавить к ответу:
Задание 1 — найти произведение чисел 202 и 123. Решение таково:
Задание 2 — вычислить 120х300. Пошаговое решение:
Операции с десятичными дробями
На самом деле умножение десятичных дробей столбиком не слишком сильно отличается от аналогичного действия с числами, у которых есть нули.
В этом случае примеры решают точно так же, как и обычные — про запятую можно временно забыть. Но, когда ответ уже найден, её обязательно нужно восстановить. А для этого надо узнать, сколько цифр после запятой находится у каждого множителя. Их количество складывают, а потом отсчитывают это число с конца ответа.
Задание 1 — вычислить 2,5х3. Пошаговое решение:
Задание 2 — отыскать значение произведения 7,5х2,5. Решение с объяснением:
Если как следует разобраться в теме, юный математик сможет решать даже сложные примеры. Единственный минус метода — большие числа делают вычисления громоздкими, из-за каждой ошибки придётся проверять и править весь пример.
Умножение натуральных чисел столбиком: примеры, решения
Если нам по ходу решения задачи требуется перемножить натуральные числа, удобно использовать для этого готовый способ, который называется «умножение в столбик» (или «умножение столбиком»). Это очень удобно, поскольку с его помощью можно свести умножение многозначных чисел к последовательному перемножению однозначных.
В этом материале мы расскажем, как считать с помощью данного способа. Все пояснения будут проиллюстрированы примерами решений задач.
Основы умножения столбиком
Для ведения вычисления в столбик нам будет нужна таблица умножения. Важно помнить ее наизусть, чтобы считать быстро и эффективно.
Также потребуется вспомнить, какой результат мы получим при умножении натурального числа на нуль. Это часто встречается в примерах. Нам потребуется свойство умножения, которое в буквенном виде записывается как a · 0 = 0 ( a – любое натуральное число).
Чтобы лучше понять, как умножать столбиком, рекомендуем вам повторить аналогичный метод сложения. Один из этапов подсчетов будет представлять собой именно сложение промежуточных результатов, и знание этого метода при складывании чисел нам пригодится.
Также важно, чтобы вы умели сравнивать натуральные числа и помнили, что такое разряд.
Как записывать множители при подсчете столбиком
Как всегда, начнем с того, как правильно записать исходные числа. Нам нужно взять два множителя и записать их один под другим так, чтобы все цифры, отличные от нуля, были расположены друг под другом. Проведем под ними горизонтальную линию, отделяющую ответ, и добавим знак умножения с левой стороны.
Далее нам нужно разобраться с процессом умножения. Для начала посмотрим, как правильно умножать многозначное натуральное число на однозначное, а потом посмотрим, как перемножать между собой многозначные числа.
Как умножить столбиком многозначное число на однозначное
Если нам для решения задачи требуется выполнить умножение двух натуральных чисел, одно из которых однозначное, а второе многозначное, то мы можем использовать способ столбика. Для этого выполняем последовательность шагов, которую будем объяснять сразу на примере. Сначала возьмем задачу, в которой многозначное число имеет в конце цифру, отличную от нуля.
Решение
Запишем множители так, как это предполагает метод умножения столбиком. Поместим однозначный множитель под последним знаком многозначного. Мы получили такую запись:
Далее нам надо выполнить последовательное перемножение разрядов многозначного числа на указанный множитель. Если у нас получается число, которое меньше десяти, мы сразу вносим его в поле ответа под горизонтальной чертой, строго под вычисляемым разрядом. Если же результат составил 10 и больше, то указываем под нужным разрядом только значение единиц из полученного числа, а десятки запоминаем и добавляем на следующем шаге к более старшему разряду.
На конкретных числах процесс будет выглядеть так:
3. Дальше действуем аналогично. Теперь нам надо умножить значения разряда сотен в первом многозначном множителе на исходный однозначный. Порядок действий тот же: если запоминали число на предыдущем этапе, плюсуем его к результату, сравниваем с десяткой и записываем в правильное место.
4. Переходим к следующему разряду – умножаем тысячи. Продолжаем подсчеты по алгоритму до тех пора, пока не кончатся цифры в многозначном множителе.
У нас больше не осталось разрядов, которые надо перемножить, однако единица в запасе все еще есть. Мы просто запишем ее под горизонтальную черту с левой стороны от всех уже имеющихся там цифр:
Процесс подсчета с помощью столбика на этом завершен. Мы получили шестизначное число, которое и является верным решением нашей задачи.
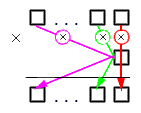
Чтобы было более понятно, мы представили алгоритм умножения многозначного натурального числа на однозначное в виде схемы. Здесь верно отражена самая суть процесса подсчета, однако не учтены некоторые нюансы:
Как быть, если в условии задачи стоит многозначное число, которое заканчивается нулем (или несколькими нулями подряд)? Рассмотрим на примере пошагово. Чтобы было проще, позаимствуем цифры из предыдущей задачи и просто допишем к исходному многозначному множителю пару нулей.
Решение
Cначала запишем числа нужным способом.
После этого проводим подсчеты, не обращая внимания на нули справа. Возьмем результаты из предыдущей задачи, чтобы не считать еще раз:
Финальный шаг решения – переписать имеющиеся в многозначном числе нули под горизонтальную черту в область результата. У нас нужно внести 2 дополнительных нуля:
Это число и будет ответом нашей задачи. На этом умножение столбиком завершено.
Как перемножить столбиком два многозначных натуральных числа
Этот способ вполне подходит и для тех случаев, когда оба множителя представляют собой многозначные натуральные числа. Разберем процесс сразу на примере, как и раньше. Сначала возьмем числа без нулей в конце, а потом рассмотрим и записи с нулями.
Решение
Начинаем последовательно перемножать значения разрядов. При этом у нас будут получаться результаты, которые называются неполными произведениями.
3. Последующие шаги выполняем аналогично, перемножая по очереди значения нужных разрядов (если они не равны 0 ). Вносим результаты под черту.
Итак, нам надо умножить 8 063 на значения сотен в 207 (т.е. на два). Мы получили второе неполное произведение, запишем его так:
Получившееся под чертой семизначное число – это и есть нужный нам результат умножения исходных натуральных чисел.
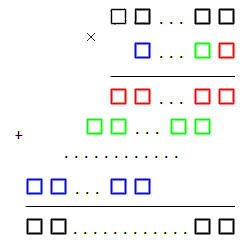
Процесс умножения двух многозначных чисел столбиков также можно представить в виде наглядной схемы:
Чтобы лучше закрепить материал, приведем решение еще одного примера.
Решение
Начинаем с правильной записи множителей. Количество знаков в них одинаковое, так что порядок записи особого значения не имеет:
3. Далее умножаем на значения сотен, т.е. 297 на 3 :
4. У нас получилось три неполных произведения, которые надо сложить (для этого желательно повторить, как правильно складывать столбиком три числа и более). Считаем:
Еще один пример приведем без пояснений.
Решение
Весь процесс вычислений указан в записи ниже.
В целом можно сказать, что если вы отлично владеете способностью умножать однозначные числа и умеете складывать столбиком, то процесс умножения многозначных натуральных чисел указанным методом не будет представлять для вас никакого труда.
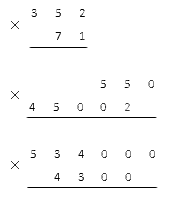
У нас остался еще один момент, который мы хотели бы пояснить. Как быть, если один из множителей или оба сразу имеет в конце нуль (или несколько нулей)? Для наглядности возьмем такую задачу и решим ее.
Решение
Все, что нам надо сделать, – это записать множители так, чтобы друг под другом оказались цифры, отличные от нуля.
Нам осталось все лишь дописать к результату оставшиеся нули. Мы добавляем их столько, сколько указано справа у обоих множителей. В нашем примере к готовому числу надо написать три нуля:
Это и будет корректный ответ.
Вычислять же значения дробей и многозначных чисел в строку бывает довольно затруднительно.
удержать промежуточные результаты в голове порой просто невозможно. Как раз для таких случаев придумано умножение в столбик — этот метод значительно упрощает математические вычисления.
Необходимый минимум
Преимущество использования «столбиков» очевидно — пропадает необходимость считать в уме или всегда держать при себе калькулятор. Даже действительно длинные числа с помощью этого метода умножаются без лишних проблем. Достаточно иметь при себе:
Если же с последним пока ещё возникают затруднения, можно положить её рядом с собой и сверять по ходу решения. Правда, при таком раскладе процесс затянется на какое-то время, а полученный результат желательно перепроверить. Ведь одна маленькая ошибка в начале или середине вычисления сделает ответ заведомо неверным.
Регулярное решение примеров столбиком тренирует внимательность и память ребёнка, учит его концентрироваться на отдельно взятой задаче. Это также удобный способ закрепить базовые математические знания.
Как умножать столбиком
Чтобы научиться решать примеры, необходимо понять и отработать базовый алгоритм.
В целом он достаточно прост:
Метод столбиков не подходит для решения примеров, содержащих корни или возведённые в степень числа.
Прежде чем приступить к вычислениям, «проблемные» цифры нужно преобразовать до целых или десятичных.
Решение базовых примеров
Для большей наглядности стоит привести примеры умножения двузначных и трёхзначных чисел.
Пример 1 — отыскать произведение чисел 58 и 23. Решение задания:
По такому же принципу происходит умножение трёхзначных чисел. Разве что вычисление потребует чуть больше времени, а количество промежуточных результатов увеличится.
Пример 2 — решить выражение 659х854. Пошаговое решение:
При затруднениях в процессе решения можно проверить правильность умножения столбиком онлайн-калькулятором. А также существуют специальные генераторы примеров, которые используют как своеобразный тренажёр для закрепления изученного материала.
Целые числа с нулями
В ситуациях с нулями немного сложнее.
Если нолик «потерялся» где-то в середине, то в процессе решения его следует пропустить. Ведь умножение абсолютно любого числа на 0 в итоге даёт этот же 0. Поэтому можно сразу переходить к следующей цифре и заполнить строку под чертой, отступив не на 1, а на 2 единицы.
Что касается таких чисел как 10, 100, 1200, 12030 и т. п. — суть такая же, но алгоритм решения отличается. Вычисления проводят лишь с цифрами, отличными от нуля. А все «0» на конце чисел просто игнорируются. Хотя после сложения их количество надо подсчитать и добавить к ответу:
Задание 1 — найти произведение чисел 202 и 123. Решение таково:
Задание 2 — вычислить 120х300. Пошаговое решение:
Операции с десятичными дробями
На самом деле умножение десятичных дробей столбиком не слишком сильно отличается от аналогичного действия с числами, у которых есть нули.
В этом случае примеры решают точно так же, как и обычные — про запятую можно временно забыть. Но, когда ответ уже найден, её обязательно нужно восстановить. А для этого надо узнать, сколько цифр после запятой находится у каждого множителя. Их количество складывают, а потом отсчитывают это число с конца ответа.
Задание 1 — вычислить 2,5х3. Пошаговое решение:
Задание 2 — отыскать значение произведения 7,5х2,5. Решение с объяснением:
Если как следует разобраться в теме, юный математик сможет решать даже сложные примеры. Единственный минус метода — большие числа делают вычисления громоздкими, из-за каждой ошибки придётся проверять и править весь пример.