Слово Как пишется уравнение касательной - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Уравнение касательной к графику функции

А что будет, если производная в точке x ₀ не существует? Возможны два варианта:

Уравнение касательной

Итак, пусть дана функция y = f ( x ), которая имеет производную y = f ’( x ) на отрезке [ a ; b ]. Тогда в любой точке x ₀ ∈ ( a ; b ) к графику этой функции можно провести касательную, которая задается уравнением:

Здесь f ’( x ₀) — значение производной в точке x ₀, а f ( x ₀) — значение самой функции.

Уравнение касательной: y = f ’( x ₀) · ( x − x ₀) + f ( x ₀). Точка x ₀ = 2 нам дана, а вот значения f ( x ₀) и f ’( x ₀) придется вычислять.

Для начала найдем значение функции. Тут все легко: f ( x ₀) = f (2) = 2 3 = 8;
Теперь найдем производную: f ’( x ) = ( x 3 )’ = 3 x 2 ;
Подставляем в производную x ₀ = 2: f ’( x ₀) = f ’(2) = 3 · 2 2 = 12;
Итого получаем: y = 12 · ( x − 2) + 8 = 12 x − 24 + 8 = 12 x − 16.
Это и есть уравнение касательной.

Задача. Составить уравнение касательной к графику функции f ( x ) = 2sin x + 5 в точке x ₀ = π /2.

В этот раз не будем подробно расписывать каждое действие — укажем лишь ключевые шаги. Имеем:

f ( x ₀) = f ( π /2) = 2sin ( π /2) + 5 = 2 + 5 = 7;
f ’( x ) = (2sin x + 5)’ = 2cos x ;
f ’( x ₀) = f ’( π /2) = 2cos ( π /2) = 0;

y = 0 · ( x − π /2) + 7 ⇒ y = 7

В последнем случае прямая оказалась горизонтальной, т.к. ее угловой коэффициент k = 0. Ничего страшного в этом нет — просто мы наткнулись на точку экстремума.

Источник

Уравнение касательной к графику функции

п.1. Уравнение касательной

п.2. Алгоритм построения касательной

На входе: уравнение кривой \(y=f(x)\), абсцисса точки касания \(x_0\).
Шаг 1. Найти значение функции в точке касания \(f(x_0)\)
Шаг 2. Найти общее уравнение производной \(f’ (x)\)
Шаг 3. Найти значение производной в точке касания \(f'(x_0 )\)
Шаг 4. Записать уравнение касательной \(y=f’ (x_0)(x-x_0)+f(x_0)\), привести его к виду \(y=kx+b\)
На выходе: уравнение касательной в виде \(y=kx+b\)

Пусть \(f(x)=x^2+3\). Найдем касательную к этой параболе в точке \(x_0=1\).

п.3. Вертикальная касательная

Не путайте вертикальные касательные с вертикальными асимптотами.
Вертикальная асимптота проходит через точку разрыва 2-го рода \(x_0\notin D\), в которой функция не определена и производная не существует. График функции приближается к асимптоте на бесконечности, но у них никогда не бывает общих точек.
А вертикальная касательная проходит через точку \(x_0\in D\), входящую в область определения. График функции и касательная имеют одну общую точку \((x_0,y_0)\).

Вертикальные касательные характерны для радикалов вида \(y=\sqrt[n]\).

Пусть \(f(x)=\sqrt[5]+1\). Найдем касательную к этой кривой в точке \(x_0=1\).

\(f(x_0)=\sqrt[5]<1-1>+1=1\)
\(f'(x)=\frac15(x-1)^<\frac15-1>+0=\frac15(x-1)^<-\frac45>=\frac<1><5(x-1)^<\frac45>> \)
\(f'(x_0)=\frac<1><5(1-1)^<\frac45>>=\frac10=+\infty\)
В точке \(x_0\) проходит вертикальная касательная.
Её уравнение: \(x=1\)
Ответ: \(y=2x+2\)

п.4. Примеры

Пример 1. Для функции \(f(x)=2x^2+4x\)
a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX.

б) Найдите, в какой точке касательная образует с положительным направлением оси OX угол 45°. Напишите уравнение этой касательной.

в) найдите, в какой точке касательная будет параллельна прямой \(2x+y-6=0\). Напишите уравнение этой касательной.

Найдем угловой коэффициент заданной прямой: \(y=-2x+6\Rightarrow k=-2\). Касательная должна быть параллельной, значит, её угловой коэффициент тоже \(k=-2\). Получаем уравнение: \begin f'(x_0)=-2\\ 4x_0+4=-2\Rightarrow 4x_0=-6\Rightarrow x_0=-\frac32 \end Точка касания \(x_0=-\frac32\) \begin f(x_0)=2\cdot\left(-\frac32\right)^2+4\cdot\left(-\frac32\right)=\\ =\frac92-6=-\frac32 \end Уравнение касательной: \begin y=-2\cdot\left(x+\frac32\right)-\frac32=-2x-\frac92 \end Или, в каноническом виде: \begin 2x+y+\frac92=0 \end

г) в какой точке функции можно провести горизонтальную касательную? Напишите уравнение этой касательной.

У горизонтальной прямой \(k=0\). Получаем уравнение: \(f'(x_0)=0\). \begin 4x_0+4=0\Rightarrow 4x_0=-4\Rightarrow x_0=-1 \end Точка касания \(x_0=-1\) \begin f(x_0)=2\cdot(-1)^2+4\cdot(-1)=-2 \end Уравнение касательной: \begin y=0\cdot(x+1)-2=-2 \end

Ответ: а) \(y=4x\) и \(y=-4x-8\); б) \(y=x-\frac98\); в) \(2x+y+\frac92=0\); г) \(y=-2\)

Пример 3*. Найдите точку, в которой касательная к графику функции \(f(x)=\frac-x\) перпендикулярна прямой \(y=11x+3\). Напишите уравнение этой касательной.

Угловой коэффициент данной прямой \(k_1=11\).
Угловой коэффициент перпендикулярной прямой \(k_2=-\frac<1>=-\frac<1><11>\) \begin f'(x)=\left(\frac\right)’-x’=\frac<2x(x+3)-(x^2+2)\cdot 1><(x+3)^2>-1=\frac<2x^2+6x-x^2-2-(x+3)^2><(x+3)^2>=\\ =\frac<(x+3)^2>=- \frac<11> <(x+3)^2>\end В точке касания: \begin f'(x_0)=k_2\Rightarrow=-\frac<11><(x+3)^2>=-\frac<1><11>\Rightarrow (x+3)^2=121\Rightarrow (x+3)^2-11^2=0\Rightarrow\\ \Rightarrow (x+14)(x+8)=0\Rightarrow \left[ \begin x=-14\\ x=8 \end \right. \end
Уравнение касательной при \(x_0=-14\) \begin f(x_0)=\frac<(-14)^2+2><-14+3>+14=\frac<198><-11>+14=-18+14=-4\\ y=-\frac<1><11>(x+14)-4=-\frac <11>\end Уравнение касательной при \(x_0=8\) \begin f(x_0)=\frac<8^2+2><8+3>-8=\frac<66><11>-8=-2\\ y=-\frac<1><11>(x-8)-2=-\frac <11>\end
Ответ: точка касания (-14;-4), уравнение \(y=-\frac<11>\)
и точка касания (8;-2), уравнение \(-\frac<11>\)

Пример 4*. Найдите уравнения общих касательных к параболам \(y=x^2-5x+6\) и \(y=x^2+x+1\). Укажите точки касания.

Пример 5*. Докажите, что кривая \(y=x^4+3x^2+2x\) не пересекается с прямой \(y=2x-1\), и найдите расстояние между их ближайшими точками.

Чтобы найти расстояние, необходимо построить касательную к кривой с тем же угловым коэффициентом \(k=2\), то и y данной прямой. Тогда искомым расстоянием будет расстояние от точки касания до прямой \(y=2x-1\).
Строим уравнение касательной. По условию: \(f'(x)=4x^3+6x+2=2\) \begin 4x^3+6x=0\Rightarrow 2x(2x^2+3)=0\Rightarrow \left[ \begin x=0\\ 2x^2+3=0 \end \right. \Rightarrow \left[ \begin x=0\\ x^2=-\frac32 \end \right. \Rightarrow \left[ \begin x=0\\ x\in\varnothing \end \right. \Rightarrow x=0 \end Точка касания \(x_0=0,\ y_0=0^4+3\cdot 0^2+2\cdot 0=0\).
Уравнение касательной: \(y=2(x-0)+0=2x\)

Ищем расстояние между двумя параллельными прямыми: \(y=2x\) и \(y=2x-1\). Перпендикуляр из точки (0;0) на прямую \(y=2x-1\) имеет угловой коэффициент \(k=-\frac12\), его уравнение: \(y=-\frac12 x+b\). Т.к. точка (0;0) принадлежит этому перпендикуляру, он проходит через начало координат и \(b=0\).

Уравнение перпендикуляра: \(y=-\frac x2\).
Находим точку пересечения прямой \(y=2x-1\) и перпендикуляра \(y=-\frac x2\): \begin 2x-1=-\frac x2\Rightarrow 2,5x=1\Rightarrow x=0,4;\ y=-\frac<0,4><2>=-0,2 \end Точка пересечения A(0,4;-0,2).
Находим расстояние \(OA=\sqrt<0,4^2+(-0,2)^2>=0,2\sqrt<2^2+1^2>=\frac<\sqrt<5>><5>\)
Ответ: \(\frac<\sqrt<5>><5>\)

Источник

Уравнение касательной и уравнение нормали к графику функции

Как получить уравнение касательной и уравнение нормали

Уравнение касательной выводится из уравнения прямой.

Отсюда получаем следующую запись:

Таким образом, можем заменить k на f ‘(x 0 ) и получить следующее уравнение касательной к графику функции:

В задачах на составление уравнения касательной к графику функции (а мы уже скоро к ним перейдём) требуется привести получившееся по вышеприведённой формуле уравнение к уравнению прямой в общем виде. Для этого нужно все буквы и числа перенести в левую часть уравнения, а в правой части оставить ноль.

Переходим к примерам. Для решений потребуется таблица производных (откроется в новом окне).

Для разминки первый же пример прелагается решить самостоятельно, а затем посмотреть решение. Есть все основания надеяться, что для наших читателей эта задача не будет «холодным душем».

Решаем задачи вместе

Пример 1. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

Найдём производную функции:

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем

В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:

На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.

Пример 2. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

Найдём производную функции:

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Подставляем все полученные данные в «формулу-болванку» и получаем уравнение касательной:

Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):

Составляем уравнение нормали:

Пример 3. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

Найдём производную функции:

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Находим уравнение касательной:

Перед тем, как привести уравнение к общему виду, нужно его немного «причесать»: умножить почленно на 4. Делаем это и приводим уравнение к общему виду:

Составляем уравнение нормали:

Решить задачи самостоятельно, а затем посмотреть решения

Пример 4. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Пример 5. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Снова решаем задачи вместе

Пример 6. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

Найдём производную функции:

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Получаем уравнение касательной:

Приводим уравнение к общему виду:

Составляем уравнение нормали:

Пример 7. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Получаем уравнение касательной:

Приводим уравнение к общему виду:

Составляем уравнение нормали:

Пример 8. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Источник

Решение уравнения касательной через график производной функции

Геометрический смысл производной функции в точке

Вывод формулы имеет следующий вид:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Графически производную можно изобразить в виде кривой таким образом:

Разберем типичный пример в доказательство определению. Попробуем найти производную записанным ранее методом \((x^2+1)\) :

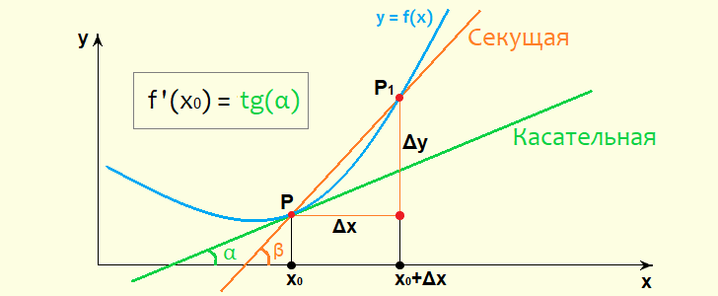
Согласно историческим фактам, одновременно с написанием работы Ньютона по изучению процессов в физике и формулировке понятия производной Лейбницем было введено определение производной с помощью геометрических закономерностей. Узнать, в чем состоит геометрический смысл производной, можно с помощью исследования графика функции y=f(x) на плоскости:

Приращение функции относится к приращению аргумента, как тангенс угла, образованный секущей и положительным направлением оси абсцисс:

Когда значение \(\triangle x\) стремится к нулю, точка Р1 на изображенном графике смещается в сторону точки Р. Положение секущей в таком случае меняется по отношению к графику.

Секущая занимает предельное положение в виде прямой, когда приращение стремится к нулю. Точки Р и Р1 на данной прямой будут совмещены. Рассматриваемая прямая является касательной к графику в точке Р.

Запишем следующее соотношение:

\(tg\beta \rightarrow tg\alpha, если \triangle x\rightarrow 0\)

Геометрический смысл производной: производная функции в точке обладает значением, численно равным тангенсу угла наклона касательной к функции в рассматриваемой точке.

Известным фактом является то, что какая-либо прямая обладает уравнением, которое можно записать в общем виде:

В уравнении касательной к функции в некой точке Р коэффициент k определяется, как значение производной в точке х0:

В процессе решения практических заданий нередко можно встретить примеры, где требуется использовать геометрический смысл производной. Одной из подобных задач является изучение графически заданной функции в сравнении с графиком производной искомой функции.

Уравнение касательной к графику функций

В результате угловой коэффициент касательной будет определен по формуле:

В качестве наглядного примера изобразим график по исходным данным:

Алгоритм составления уравнения касательной к графику функции

Составить уравнение, с помощью которого задана касательная к графику функции, несложно. Нужно лишь следовать следующему алгоритму и выполнять действия в таком порядке:

Рассмотрим конкретный пример. Попробуем составить уравнение касательной к функции \(f\left( x \right)=<^<2>>-2x+3.\) Выполним действия последовательно, руководствуясь записанным ранее алгоритмом:

Примеры решения задач

Функция \( y=\mathsf\left( x \right)\) изображена графически. На этом же правильном графике построена касательная в точке, абсцисса которой равна \(_<0>.\)

Согласно определению значения производной в точке касания, запишем:

\(f’\left( x \right)=k=\ \varphi\)

В результате значение производной функции \(\mathsf\left( x \right)\) в точке \(<_<0>>\) соответствует 1,2.

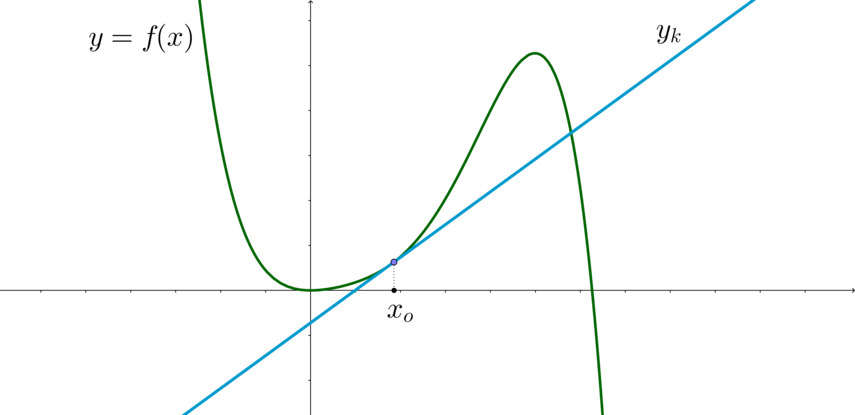
Изображено два графика функций:

Нужно вычислить все значения, которые принимает параметр а при пересечении рассматриваемых графиков только в одной точке.

Функция \(f(x)\) на графике будет иметь вид параболы, пересекающей ось абсцисс в следующих точках:

Данная парабола имеет одну точку пересечения с осью ординат:

Если зафиксировать а, то при каждом таком значении \(ay+5x+6a=0\) будет иметь вид прямой:

В результате графики обладают единственной общей точкой при таких значениях a, при которых прямая y будет касаться параболы. Касание в точке \(x_o\) возможно при следующих условиях:

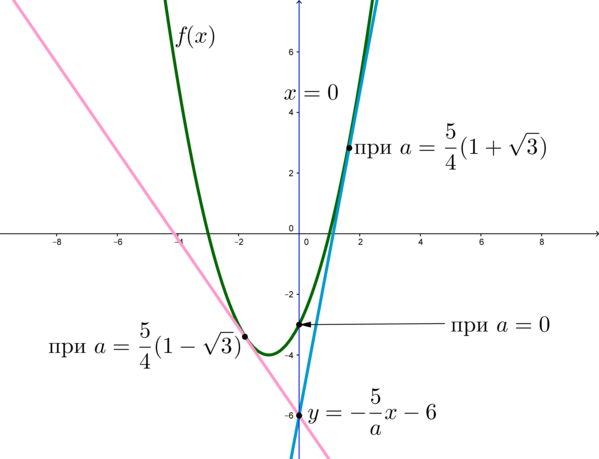
Имеется некое уравнение:

Требуется определить все вероятные значения, которыми обладает параметр а, определяющие для данного уравнения единственное решение.

Проанализируем функцию и пучок, состоящий из прямых:

Точка максимума равна:

Точка минимума равна:

Запишем следующие соотношения:

Каждая из прямых \(y=ax+8a\) пересекает точку (-8;0). Выявим такие случаи, при которых прямая у будет касаться графика функции f(x) в точке касания \(x_o.\) Подберем под заданные условия значения параметра:

\(\begin f'(x_o)=a\\ f(x_o)=y(x_o) \end \Rightarrow \begin x_o^2+4x_o=a\\ 2x_o^3+30x_o^2+96x_o+88=0 \end\Rightarrow \begin x_o^2+4x_o=a\\ (x_o+2)^2(x_o+11)=0 \end \Rightarrow \left[ \begin \begin &\begin x_o=-2\\ a=-4 \end\\ &\begin x_o=-11\\ a=77 \end \end \end \right.\)

В результате уравнение \( f(x)=y\) обладает только одним значением, когда параметр а имеет значения, при которых прямые y проходят в заштрихованных участках. Отметим, что граничный случай a=77 является посторонним.

График в уменьшенном масштабе:

Ответ: \(a\in (-\infty; 77).\)

Нужно найти такие значения параметра а, при которых данная система обладает только одним решением.

Запишем первое из уравнений, как:

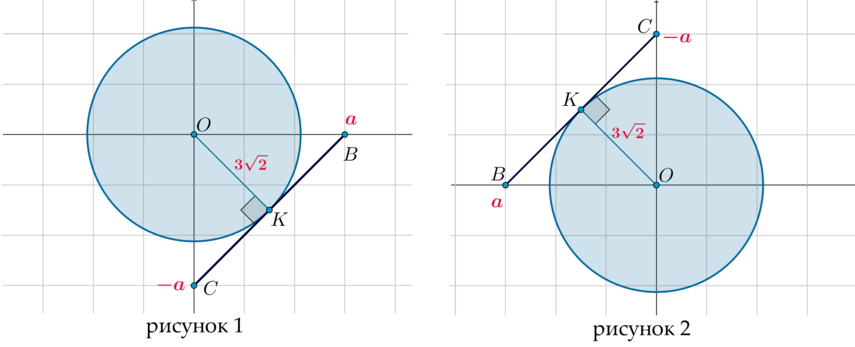
Заметим, с помощью этого уравнения можно задать множество точек А, принадлежащих отрезку ВС. Если а=0, то рассматриваемое уравнение задает только одну точку O(0;0).

С помощью второго неравенства можно изобразить окружность, центр которой находится в точке O(0;0), а ее радиус равен \(R=3\sqrt2.\)

Система будет иметь лишь одно решение при параметре а≠0 — в том случае, когда отрезок касается окружности:

\(\dfrac12\cdot OB\cdot OC=S_<\triangle OBC>=\dfrac12\cdot OK\cdot BC \quad\Rightarrow\quad a\cdot a=3\sqrt2\cdot a\sqrt2 \quad\Rightarrow\quad a=6.\)

Источник