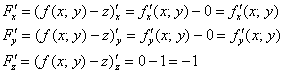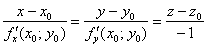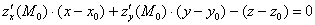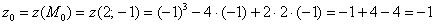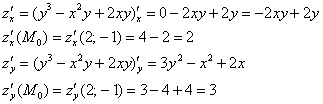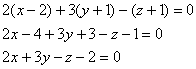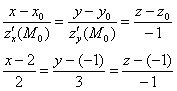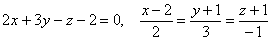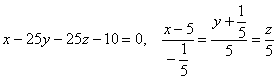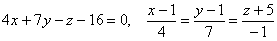Касательная и нормаль к графику функции
Основные формулы
Определения
Здесь мы приводим определения, которые встречаются в литературе, и имеют отношение к касательной и нормали. Вывод формул приводится в примере 1 ⇓.
Определение касательной приводится здесь. Уравнение касательной:
.
Полезные формулы из аналитической геометрии
Далее приводятся некоторые сведения из аналитической геометрии, которые могут оказаться полезными при решении задач.
Уравнение прямой, проходящей через две заданные точки и :
.
Здесь – направляющий вектор прямой.
Уравнение прямой, проходящей через точку параллельно вектору имеет вид:
.
Вектор называется направляющим вектором данной прямой. Это уравнение можно написать в параметрическом виде, введя параметр t :
Уравнение прямой, проходящей через точку перпендикулярно вектору имеет вид:
.
Вектор называется вектором нормали данной прямой.
Уравнение прямой в отрезках, пересекающей оси координат в точках :
.
Примеры решения задач
Пример 1
Находим значение функции при :
.
Находим производную:
.
Находим производную в точке :
;
.
Касательная и нормаль к графику функции y=x 2 в точке M0(1;1).
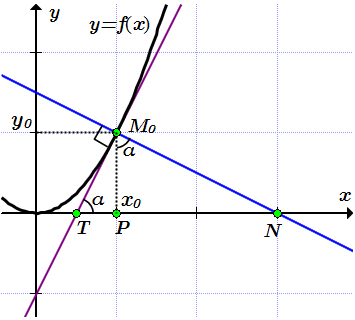
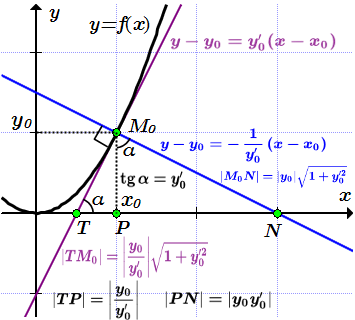
Найдем угол α между касательной и осью абсцисс по формуле (1):
.
Подставляем :
;
.
Примечание.
При выводе формул, можно сначала определить длины отрезков подкасательной и поднормали, а затем из прямоугольников, по теореме Пифагора, найти длины отрезков касательной и нормали:
;
.
Пример 2
Касательная и нормаль к циссоиде в точке (2;2).
Пример 3
Находим уравнение касательной по формуле (2).
;
;
;
.
Находим уравнение нормали по формуле (3).
;
;
;
.
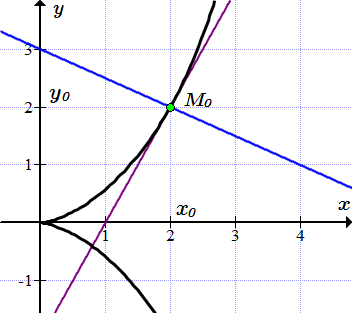
Касательная и нормаль к циссоиде изображены на рисунке ⇑.
Пример 4
Ниже приводятся графики функций ⇓ и вывод формулы угла между кривыми.
Вывод формулы для угла между кривыми
Этот случай изображен на рисунке ⇑.
Использованная литература:
П.Е. Данько, А.Г. Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах. Часть 1. Москва, Высшая школа, 1980.
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, Физматлит, 2003.
Уравнение касательной и уравнение нормали к графику функции
Как получить уравнение касательной и уравнение нормали
Уравнение касательной выводится из уравнения прямой.
Отсюда получаем следующую запись:
Таким образом, можем заменить k на f ‘(x 0 ) и получить следующее уравнение касательной к графику функции:
В задачах на составление уравнения касательной к графику функции (а мы уже скоро к ним перейдём) требуется привести получившееся по вышеприведённой формуле уравнение к уравнению прямой в общем виде. Для этого нужно все буквы и числа перенести в левую часть уравнения, а в правой части оставить ноль.
Переходим к примерам. Для решений потребуется таблица производных (откроется в новом окне).
Для разминки первый же пример прелагается решить самостоятельно, а затем посмотреть решение. Есть все основания надеяться, что для наших читателей эта задача не будет «холодным душем».
Решаем задачи вместе
Пример 1. Составить уравнение касательной и уравнение нормали к графику функции 
, если абсцисса точки касания 
.
Решение. Найдём ординату точки касания:
.
Найдём производную функции:
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем
В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:
На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.
Пример 2. Составить уравнение касательной и уравнение нормали к графику функции 
, если абсцисса точки касания 
.
Решение. Найдём ординату точки касания:
.
Найдём производную функции:
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Подставляем все полученные данные в «формулу-болванку» и получаем уравнение касательной:
Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):
Составляем уравнение нормали:
Пример 3. Составить уравнение касательной и уравнение нормали к графику функции 
, если абсцисса точки касания 
.
Решение. Найдём ординату точки касания:
.
Найдём производную функции:
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Находим уравнение касательной:
Перед тем, как привести уравнение к общему виду, нужно его немного «причесать»: умножить почленно на 4. Делаем это и приводим уравнение к общему виду:
Составляем уравнение нормали:
Решить задачи самостоятельно, а затем посмотреть решения
Пример 4. Составить уравнение касательной и уравнение нормали к графику функции 
, если абсцисса точки касания 
.
Пример 5. Составить уравнение касательной и уравнение нормали к графику функции 
, если абсцисса точки касания 
.
Снова решаем задачи вместе
Пример 6. Составить уравнение касательной и уравнение нормали к графику функции 
, если абсцисса точки касания 
.
Решение. Найдём ординату точки касания:
.
Найдём производную функции:
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Получаем уравнение касательной:
Приводим уравнение к общему виду:
Составляем уравнение нормали:
Пример 7. Составить уравнение касательной и уравнение нормали к графику функции 
, если абсцисса точки касания 
.
Решение. Найдём ординату точки касания:
.
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Получаем уравнение касательной:
Приводим уравнение к общему виду:
Составляем уравнение нормали:
Пример 8. Составить уравнение касательной и уравнение нормали к графику функции 
, если абсцисса точки касания 
.
Решение. Найдём ординату точки касания:
.
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Как найти уравнения касательной плоскости и нормали
к поверхности в заданной точке?
Сегодня на уроке я расскажу вам об одном популярном приложении дифференциального исчисления функции двух переменных, а именно, о том, что вы видите в заголовке. По существу, это «пространственный аналог» задачи нахождения касательной и нормали к графику функции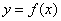 
одной переменной, и поэтому никаких трудностей возникнуть не должно.
Начнём с базовых вопросов: ЧТО ТАКОЕ касательная плоскость и ЧТО ТАКОЕ нормаль? Многие осознают эти понятия на уровне интуиции. Самая простая модель, приходящая на ум – это шар, на котором лежит тонкая плоская картонка. Картонка расположена максимально близко к сфере и касается её в единственной точке. Кроме того, в точке касания она закреплена торчащей строго вверх иголкой.
В теории существует довольно остроумное определение касательной плоскости. Представьте произвольную поверхность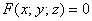 
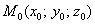
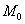
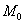
и принадлежащую ей точку 
. Очевидно, что через точку 
проходит много пространственных линий, которые принадлежат данной поверхности. У кого какие ассоциации? =) …лично я представил осьминога. Предположим, что у каждой такой линии существует пространственная касательная в точке 
.
Определение 1: касательная плоскость к поверхности в точке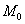 
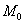
– это плоскость, содержащая касательные ко всем кривым, которые принадлежат данной поверхности и проходят через точку 
.
Определение 2: нормаль к поверхности в точке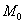 
– это прямая, проходящая через данную точку перпендикулярно касательной плоскости.
Просто и изящно. Кстати, чтобы вы не померли со скуки от простоты материала, чуть позже я поделюсь с вами одним изящным секретом, который позволяет РАЗ И НАВСЕГДА забыть о зубрёжке различных определений.
С рабочими формулами и алгоритмом решения познакомимся прямо на конкретном примере. В подавляющем большинстве задач требуется составить и уравнение касательной плоскости, и уравнения нормали:
Найти уравнения касательной плоскости и нормали к поверхности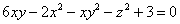 
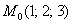
в точке 
.
Решение: если поверхность задана уравнением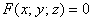 
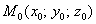
(т.е. неявно), то уравнение касательной плоскости к данной поверхности в точке 
можно найти по следующей формуле: 
Особое внимание обращаю на необычные частные производные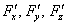 
– их не следует путать с частными производными неявно заданной функции (хотя поверхность задана неявно). При нахождении этих производных нужно руководствоваться правилами дифференцирования функции трёх переменных, то есть, при дифференцировании по какой-либо переменной, две другие буквы считаются константами: 
Не отходя от кассы, найдём частную производную в точке: 
Аналогично: 
Это был самый неприятный момент решения, в котором ошибка если не допускается, то постоянно мерещится. Тем не менее, здесь существует эффективный приём проверки, о котором я рассказывал на уроке Производная по направлению и градиент.
Все «ингредиенты» найдены и теперь дело за аккуратной подстановкой с дальнейшими упрощениями: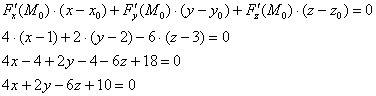 
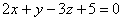
– общее уравнение искомой касательной плоскости.
Настоятельно рекомендую проконтролировать и этот этап решения. Сначала нужно убедиться, что координаты точки касания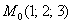 
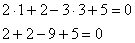
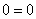
действительно удовлетворяют найденному уравнению: 
– верное равенство.
Теперь «снимаем» коэффициенты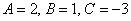 
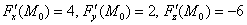
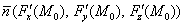
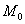
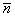
общего уравнения плоскости и проверяем их на предмет совпадения либо пропорциональности с соответствующими значениями 
. В данном случае пропорциональны. Как вы помните из курса аналитической геометрии, 
– это вектор нормали касательной плоскости, и он же – направляющий вектор нормальной прямой. Составим канонические уравнения нормали по точке 
и направляющему вектору 
: 
В принципе, знаменатели можно сократить на «двойку», но особой надобности в этом нет
Ответ: 
Уравнения не возбраняется обозначить какими-нибудь буквами, однако, опять же – зачем? Здесь и так предельно понятно, что к чему.
Следующие два примера для самостоятельного решения. Небольшая «математическая скороговорка»:
Найти уравнения касательной плоскости и нормали к поверхности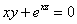 
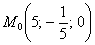
в точке 
.
И задание, интересное с технической точки зрения:
Составить уравнения касательной плоскости и нормали к поверхности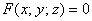 
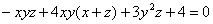
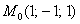
в точке 
в точке 
.
Тут есть все шансы не только запутаться, но и столкнуться с трудностями при записи канонических уравнений прямой. А уравнения нормали, как вы, наверное, поняли, принято записывать именно в таком виде. Хотя, по причине забывчивости либо незнания некоторых нюансов более чем приемлема и параметрическая форма.
Примерные образцы чистового оформления решений в конце урока.
В любой ли точке поверхности существует касательная плоскость? В общем случае, конечно же, нет. Классический пример – это коническая поверхность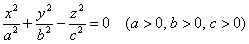 
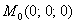
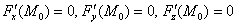
и точка 
– касательные в этой точке непосредственно образуют коническую поверхность, и, разумеется, не лежат в одной плоскости. В неладах легко убедиться и аналитически: 
.
Другим источником проблем является факт несуществования какой-либо частной производной в точке. Однако это ещё не значит, что в данной точке нет единой касательной плоскости.
Но то была, скорее, научно-популярная, нежели практически значимая информация, и мы возвращаемся к делам насущным:
Как составить уравнения касательной плоскости и нормали в точке,
если поверхность задана явной функцией 
?
?Перепишем её в неявном виде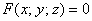 
:
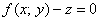
и по тем же принципам найдём частные производные: 
Таким образом, формула касательной плоскости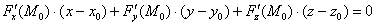 
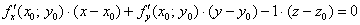
трансформируется в следующее уравнение:
, и соответственно, канонические уравнения нормали:
Как нетрудно догадаться,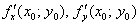 
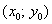
– это уже «настоящие» частные производные функции двух переменных в точке 
, которые мы привыкли обозначать буквой «зет» и находили 100500 раз.
Заметьте, что в данной статье достаточно запомнить самую первую формулу, из которой в случае необходимости легко вывести всё остальное (понятно, обладая базовым уровнем подготовки). Именно такой подход следует использовать в ходе изучения точных наук, т.е. из минимума информации надо стремиться «вытаскивать» максимум выводов и следствий. «Соображаловка» и уже имеющиеся знания в помощь! Этот принцип полезен ещё и тем, что с большой вероятностью спасёт в критической ситуации, когда вы знаете очень мало.
Отработаем «модифицированные» формулы парой примеров:
Составить уравнения касательной плоскости и нормали к поверхности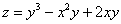 
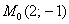
в точке 
.
Небольшая тут накладка получилась с обозначениями – теперь буква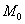 
обозначает точку плоскости 
, но что поделать – такая уж популярная буква….
Решение: уравнение искомой касательной плоскости составим по формуле: 
Вычислим значение функции в точке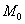 
: 
Вычислим частные производные 1-го порядка в данной точке: 
Таким образом: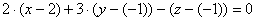 
аккуратно, не спешим: 
Запишем канонические уравнения нормали в точке 
:
Ответ: 
И заключительный пример для самостоятельного решения:
Составить уравнения касательной плоскости и нормали к поверхности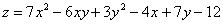 
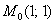
в точке 
.
Заключительный – потому, что фактически все технические моменты я разъяснил и добавить особо нечего. Даже сами функции, предлагаемые в данном задании, унылы и однообразны – почти гарантированно на практике вам попадётся «многочлен», и в этом смысле Пример №2 с экспонентой смотрится «белой вороной». Кстати, гораздо вероятнее встретить поверхность, заданную уравнением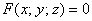 
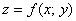
и это ещё одна причина, по которой функция 
вошла в статью «вторым номером».
И напоследок обещанный секрет: так как же избежать зубрёжки определений? (я, конечно, не имею в виду ситуацию, когда студент что-то лихорадочно зубрит перед экзаменом)
Определение любого понятия/явления/объекта, прежде всего, даёт ответ на следующий вопрос: ЧТО ЭТО ТАКОЕ? (кто/такая/ такой/такие). Осознанно отвечая на данный вопрос, вы должны постараться отразить существенные признаки, однозначно идентифицирующие то или иное понятие/явление/объект. Да, поначалу это получается несколько косноязычно, неточно и избыточно (препод поправит =)), но со временем развивается вполне достойная научная речь.
Потренируйтесь на самых отвлечённых объектах, например, ответьте на вопрос: кто такой Чебурашка? Не так-то всё просто 😉 Это «сказочный персонаж с большими ушами, глазами и коричневой шерстью»? Далеко и очень далеко от определения – мало ли существует персонажей с такими характеристиками…. А вот это уже гораздо ближе к определению: «Чебурашка – это персонаж, придуманный писателем Эдуардом Успенским в 1966 г, который …(перечисление основных отличительных признаков)». Обратите внимание, как грамотно начата статья о Чебурашке в Википедии – с понятия, кто это такой.
Кроме того, в прикладных областях особую важность приобретает второй вопрос: ЗАЧЕМ ЭТО НУЖНО? Например, та или иная команда языка программирования. В подобных определениях должен обязательно содержаться ответ на этот вопрос.
Однако ответ желательно найти в любом случае. Ну, с нашими примерами всё понятно, Чебурашка нужен, чтобы развлекать детей, а касательные плоскости и нормали – чтобы радовать взрослых =)
Эту статью я написал за один-единственный день (величайшая редкость), и надеюсь, она вам понравилась!
Традиционные решения и ответы:
Пример 2: Решение: уравнение касательной плоскости к поверхности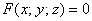 
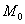
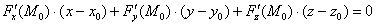
в точке 
составим по формуле: 
Вычислим частные производные в точке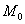 
: 
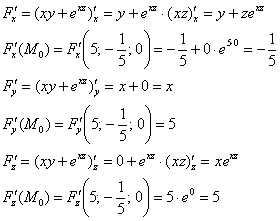
Таким образом: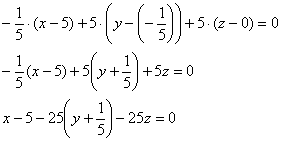 
(умножили обе части на –5)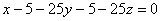 
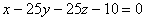
– уравнение искомой касательной плоскости.
Запишем уравнения нормали к поверхности в точке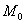 
: 
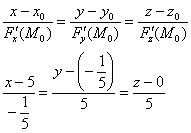
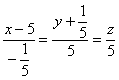
– канонические уравнения искомой нормали.
Ответ: 
Пример 3: Решение: преобразуем уравнение: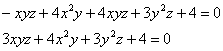 
Вычислим частные производные в точке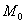 
: 
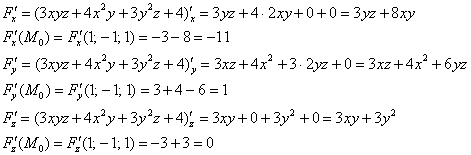
Запишем уравнение касательной плоскости к данной поверхности в точке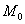 
: 
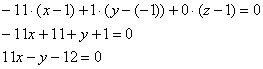
Запишем канонические уравнения нормали в точке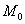 
: 
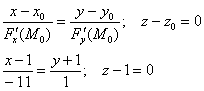
Ответ: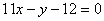 
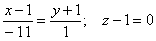
– уравнение искомой касательной плоскости;
– уравнения искомой нормали.
Пример 5: Решение: используем формулу: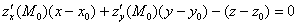 
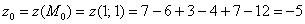
Вычислим частные производные в точке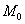 
: 
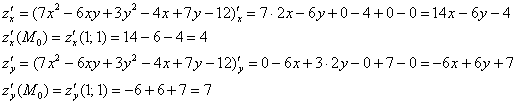
Таким образом, уравнение касательной плоскости к поверхности в точке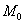 
: 
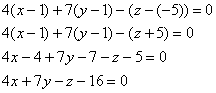
Уравнения нормали: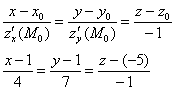 
Ответ: 
Автор: Емелин Александр
(Переход на главную страницу)
Zaochnik.com – профессиональная помощь студентам
cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5
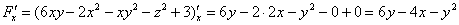
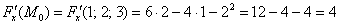
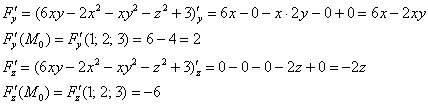
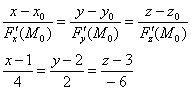
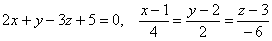
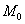
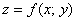