ЧЕТЫРЕХУГОЛЬНИК
Смотреть что такое ЧЕТЫРЕХУГОЛЬНИК в других словарях:
ЧЕТЫРЕХУГОЛЬНИК
частный случай многоугольника (см.). Он называется плоским, если его вершины лежат в одной плоскости; в противном же случае Ч. называется косым. В данн. смотреть
ЧЕТЫРЕХУГОЛЬНИК
четырёхугольник м. 1) Геометрическая фигура, ограниченная замкнутой ломаной линией, образующей четыре угла. 2) Пространство или предмет такой формы.
ЧЕТЫРЕХУГОЛЬНИК
четырёхугольник м.quadrangle; (квадрат) square
ЧЕТЫРЕХУГОЛЬНИК
ЧЕТЫРЕХУГОЛЬНИК
Четырехугольник — частный случай многоугольника (см.). Он называется плоским, если его вершины лежат в одной плоскости; в противном же случае Ч. называ. смотреть
ЧЕТЫРЕХУГОЛЬНИК
ЧЕТЫРЕХУГОЛЬНИК
ЧЕТЫРЕХУГОЛЬНИК
quadrilateral* * *четырёхуго́льник м.quadrangle, quadrilateral, tetragon; (на диаграмме) boxгеодези́ческий четырёхуго́льник — geodetic quadrangle, br. смотреть
ЧЕТЫРЕХУГОЛЬНИК
ЧЕТЫРЕХУГОЛЬНИК
1) quadrangle2) <geom.> quadrilateral3) tetragon– геодезический четырехугольник– неплоский четырехугольник– полный четырехугольникСинонимы: анти. смотреть
ЧЕТЫРЕХУГОЛЬНИК
четырёхугольник м геом quadrilátero m; quadrângulo mСинонимы: антипараллелограм, каре, многоугольник, параллелограмм, прямоугольник, тетрагон, трапеце. смотреть
ЧЕТЫРЕХУГОЛЬНИК
m.quadrangleСинонимы: антипараллелограм, каре, многоугольник, параллелограмм, прямоугольник, тетрагон, трапецея, трапеция, четыреугольник
ЧЕТЫРЕХУГОЛЬНИК
м.carré m; геом. tétragone m, quadrilatère mСинонимы: антипараллелограм, каре, многоугольник, параллелограмм, прямоугольник, тетрагон, трапецея, трап. смотреть
ЧЕТЫРЕХУГОЛЬНИК
мViereck nСинонимы: антипараллелограм, каре, многоугольник, параллелограмм, прямоугольник, тетрагон, трапецея, трапеция, четыреугольник
ЧЕТЫРЕХУГОЛЬНИК
firkant, karréСинонимы: антипараллелограм, каре, многоугольник, параллелограмм, прямоугольник, тетрагон, трапецея, трапеция, четыреугольник
ЧЕТЫРЕХУГОЛЬНИК
négyszögСинонимы: антипараллелограм, каре, многоугольник, параллелограмм, прямоугольник, тетрагон, трапецея, трапеция, четыреугольник
ЧЕТЫРЕХУГОЛЬНИК
м. quadrangolo, quadrilatero m, tetragono Итальяно-русский словарь.2003. Синонимы: антипараллелограм, каре, многоугольник, параллелограмм, прямоугольник, тетрагон, трапецея, трапеция, четыреугольник. смотреть
ЧЕТЫРЕХУГОЛЬНИК
четырехугольникViereckСинонимы: антипараллелограм, каре, многоугольник, параллелограмм, прямоугольник, тетрагон, трапецея, трапеция, четыреугольник
ЧЕТЫРЕХУГОЛЬНИК
ЧЕТЫРЕХУГОЛЬНИК
ЧЕТЫРЕХУГОЛЬНИК м. 1) Геометрическая фигура, ограниченная замкнутой ломаной линией, образующей четыре угла. 2) Пространство или предмет такой формы.
ЧЕТЫРЕХУГОЛЬНИК
четырехугольник четырехсторонник, каре, параллелограмм, трапеция, прямоугольник, четыреугольник, многоугольник, трапецея, тетрагон
ЧЕТЫРЕХУГОЛЬНИК
сущ. муж. родачотирикутник
ЧЕТЫРЕХУГОЛЬНИК
ЧЕТЫРЕХУГОЛЬНИК
ЧЕТЫРЁХУГОЛЬНИК четырёхугольника, м. Геометрическая фигура, имеющая четыре угла.
Правильный четырёхугольник
Это статья о геометрической фигуре. Другие значения слова см. на странице Квадрат (значения).
Свойства
См. также
| Правильные многоугольники |
|---|
| Треугольник | Четырёхугольник | Пятиугольник | Шестиугольник | Семиугольник | Восьмиугольник | Девятиугольник | Семнадцатиугольник | 257-угольник | 65537-угольник |
| (См. также: Многоугольник, Теорема Гаусса — Ванцеля) |
Полезное
Смотреть что такое «Правильный четырёхугольник» в других словарях:
Правильный четырехугольник — Это статья о геометрической фигуре. Другие значения слова см. на странице Квадрат (значения). Квадрат Квадрат правильный четырёхугольник. Свойства Квадрат может быть определён как прямоугольник, у которого две смежные стороны равны ромб, у… … Википедия
Правильный семиугольник — Правильный семиугольник это правильный многоугольник с семью сторонами. Содержание … Википедия
Правильный 17-угольник — Правильный семнадцатиугольник геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Содержание 1… … Википедия
Правильный 65537-угольник — 65537 угольник или окружность? Правильный 65537 угольник (шестѝдесятипятиты̀сячпятисо̀ттридцатисемиугольник) геометрическая фигура из группы правильных многоугольников, состоящая из 65537 … Википедия
Правильный 257-угольник — 257 угольник или окружность? Правильный 257 угольник правильный многоугольник с 257 сторонами. Содержание … Википедия
правильный — I пра/вильный ая, ое; лен, льна, льно. см. тж. правильность 1) а) Соответствующий установленным правилам, не отступающий от существующих правил, норм, порядка. П ое произношение, написание. П ое физическое развитие ребёнка. П ое распределение… … Словарь многих выражений
правильный — I. ПРАВИЛЬНЫЙ ая, ое; лен, льна, льно. 1. Соответствующий установленным правилам, не отступающий от существующих правил, норм, порядка. П ое произношение, написание. П ое физическое развитие ребёнка. П ое распределение энергоресурсов. Он человек… … Энциклопедический словарь
Квадрат (геометрия) — Это статья о геометрической фигуре. Другие значения слова см. на странице Квадрат (значения). Квадрат Квадрат правильный четырёхугольник. Свойства Квадрат может быть определён как прямоугольник, у которого две смежные стороны равны ромб, у… … Википедия
Квадрат — Это статья о геометрической фигуре. Другие значения слова см. на странице Квадрат (значения) Квадрат … Википедия
Поиск ответа
| Вопрос № 275891 |
Ответ справочной службы русского языка
Верно слитное написание: несшитое платье забыто.
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Возможно слитное и раздельное написание – в зависимости от значения слова совсем. См. ответ на вопрос № 272728.
Ответ справочной службы русского языка
Не с причастием пишется слитно, если у причастия нет зависимых слов; в противном случае верно раздельное написание. Ср.: непоступившие абитуриенты – не поступившие в вуз абитуриенты.
Ответ справочной службы русского языка
Правильно раздельное написание: отнюдь не верное решение ( не с прилагательными пишется раздельно при наличии слова отнюдь ).
Здравствуйте, уважаемые сотрудники «Грамоты». Очень прошу вас, помогоите. 1. Как правильно: на панели будет две новые кнопки или на панели будут две новые кнопки? (Играет ли роль наличие определения во множественном числе? Ведь без него в данном случае по Розенталю нужно «будет две нопки».) 2. Вместе или раздельно : не последнее место (значимое), не последнюю роль? Спасибо. Очень надеюсь получить ответ.
Ответ справочной службы русского языка
1. Верно: будет две новые кнопки. 2. В любом случае следует писать раздельно: не последнее.
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Первые части сложных слов аудио. и видео. пишутся слитно: аудиокнига, аудиофайл, видеоурок, видеофайл.
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Здравствуйте, Грамота. Как писать частицу «не» в этих случаях ( вместе или раздельно ): не выполнение задания, не обеспечение выполнения задания, не обеспечение порядка, не принятие мер?
Пожалуйста, ответьте срочно. Это повторный запрос.
Ответ справочной службы русского языка
Если далее не следует противопоставление, то верно слитное написание во всех указанных примерах.
Ответ справочной службы русского языка
Причастия при наличии зависимых слов пишутся с НЕ раздельно.
Ответ справочной службы русского языка
math4school.ru
Четырёхугольники
Основные определения и свойства

Четырёхугольником называется фигура, которая состоит из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.
Четырёхугольник называется выпуклым, если он расположен в одной полуплоскости относительно прямой, которая содержит любую из его сторон.
Сумма углов выпуклого четырёхугольника равна 360°:
Не существует четырёхугольников, у которых все углы острые или все углы тупые.
Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов:
Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон:
Площадь произвольного выпуклого четырёхугольника равна:

Диагоналями четырёхугольника называются отрезки, соединяющие его противолежащие вершины.
Диагонали выпуклого четырёхугольника пересекаются, а невыпуклого – нет.
Площадь произвольного выпуклого четырёхугольника:




В параллелограмме, и только в нём, середины диагоналей совпадают, и потому третья средняя линия вырождается в точку. Для других четырёхугольников средние линии – отрезки.
Все средние линии четырёхугольника пересекаются в одной точке и делятся ею пополам:
Сумма квадратов средних линий четырёхугольника равна четверти суммы квадратов всех его сторон и диагоналей:
MP 2 + NQ 2 + RS 2 = ¼ (AB 2 +BC 2 +CD 2 +AD 2 +AC 2 +BD 2 ).
Если β – угол между первой и второй средними линиями четырёхугольника, то его площадь:

Равными плитками, которые имеют форму произвольного, не обязательно выпуклого, четырёхугольника можно замостить плоскость так, чтобы не было наложений плиток друг на друга и не осталось непокрытых участков плоскости.
Описанные четырёхугольники

Четырёхугольник называется описанным около окружности (описанным), если существует такая окружность, которая касается всех его сторон, тогда сама окружность называется вписанной.
Четырёхугольник является описанным тогда и только тогда, кода суммы его противолежащих сторон равны:
Для сторон описанного четырёхугольника и радиуса вписанной в него окружности верно:
Площадь описанного четырёхугольника:
где r – радиус вписанной окружности, p – полупериметр четырёхугольника.
Площадь описанного четырёхугольника:

Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.
Точки касания вписанной окружности отсекают равные отрезки от углов четырёхугольника:
Если O – центр окружности, вписанной в четырёхугольник ABCD, то
∠AOB+∠COD = ∠BOC+∠AOD =180°.
Вписанные четырёхугольники

Четырёхугольник называется вписанным в окружность (вписанным), если существует окружность, проходящая через все его вершины, тогда сама окружность называется описанной около четырёхугольника.
Выпуклый четырёхугольник является описанным тогда и только тогда, когда сумма его противолежащих углов равна 180°:
Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

Первая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство:
Вторая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство:
Радиус окружности, описанной около четырёхугольника:
Площадь вписанного четырёхугольника:

Диагонали выпуклого четырёхугольника разбивают каждый его угол на два угла. Углы, опирающиеся на одну сторону, называются связанными углами.
Выпуклый четырёхугольник является вписанным тогда и только тогда, когда у него есть хотя бы одна пара равных связанных углов.
У вписанного четырёхугольника любые два связанных угла равны.

Если четырёхугольник одновременно является описанным и вписанным, то его площадь:
Для радиусов описанной и вписанной окружностей данного четырёхугольника и расстояния между центрами этих окружностей выполняется соотношение:
Параллелограмм

Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны:
У параллелограмма противолежащие стороны равны и противолежащие углы равны:
Сумма любых двух соседних углов параллелограмма равна 180°:
∠A +∠ B =∠ B +∠ C =∠ C +∠ D =∠ A +∠ D =180°.

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам:
Каждая диагональ делит параллелограмм на два равных треугольника:
Две диагонали параллелограмма делят его на четыре равновеликих треугольника:
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
e 2 +f 2 = a 2 +b 2 +a 2 +b 2 = 2(a 2 +b 2 ).
Высотой параллелограмма называется перпендикуляр, проведённый из вершины параллелограмма к неприлежащей стороне:
Площадь параллелограмма можно определить:

Ромбом называется параллелограмм, у которого все стороны равны:
Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов:

В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей.
Радиус окружности, вписанной в ромб, можно вычислить:
Площадь ромба можно определить:
Прямоугольник

Прямоугольником называется параллелограмм, у которого все углы прямые:

Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка:
Площадь прямоугольника можно определить:

Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали:
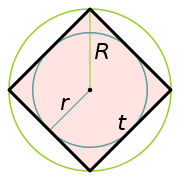
Квадрат

Квадрат – это прямоугольник, у которого все стороны равны:

Диагонали квадрата равны и перпендикулярны.
Сторона и диагональ квадрата связаны соотношениями:

У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей.
Радиус описанной окружности:
Радиус вписанной окружности:
Трапеция

Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны:
Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.

Средней линией (первой средней линией) трапеции называется отрезок, который соединяет середины боковых сторон данной трапеции:
Средняя линия трапеции параллельна её основаниям и равна их полусумме:

При продолжении до пересечения боковых сторон трапеции образуются два подобных треугольника с коэффициентом подобия, равным отношению основ:
Треугольники, образованные основами и отрезками диагоналей подобны с коэффициентом подобия, равным отношению основ:
Площади треугольников, образованных боковыми сторонами и отрезками диагоналей трапеции, равны:

Отрезок, соединяющий середины оснований (вторая средняя линия) трапеции, проходит через точку пересечения диагоналей, а его продолжение – через точку пересечения продолжений боковых сторон:
Отрезок, соединяющий середины диагоналей (третья средняя линия) трапеции, параллелен основаниям и равен их полуразности:

В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон:
Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.
В трапецию АВСD с основаниями AD и BC можно вписать окружность тогда и только тогда, когда выполняется хотя бы одно из равенств:
Боковые стороны трапеции видны из центра окружности, вписанной в данную трапецию, под прямым углом:
Радиус вписанной в трапецию окружности можно определить:

Равнобокой называется трапеция, у которой боковые стороны равны:
У равнобокой трапеции:
Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
Стороны и диагональ равнобокой трапеции связаны соотношением:

Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.

Площадь трапеции можно определить:
Дельтоид


Дельтоид называется четырёхугольник, который имеет две пары равных соседних сторон.
Дельтоид может быть выпуклым или невыпуклым.
Прямые, содержащие диагонали любого дельтоида пересекаются под прямым углом.
В любом дельтоиде углы между соседними неравными сторонами равны.
Площадь любого дельтоида можно определить:


В любой выпуклый дельтоид можно вписать окружность.
Если выпуклый дельтоид не является ромбом, то существует окружность, касающаяся продолжений всех четырёх сторон данного дельтоида.
Для невыпуклого дельтоида можно построить окружность, касающуюся двух сторон большей длины и продолжений двух меньших сторон, а также окружность, касающуюся двух меньших сторон и продолжений двух сторон большей длины.

Вокруг дельтоида можно описать окружность тогда и только тогда, когда его неравные стороны образуют углы по 90°.
Радиус окружности, описанной около дельтоида можно определить через две его неравные стороны:
Ортодиагональные четырёхугольники

Четырёхугольник называется ортодиагональным, если его диагонали пересекаются под прямым углом.
Четырёхугольник является ортодиагональным тогда и только тогда, когда выполняется одно из условий:
Сумма квадратов противолежащих сторон вписанного в окружность ортодиагонального четырёхугольника равна квадрату диаметра описанной окружности:

Ортодиагональный четырёхугольник является описанным около окружности тогда и только тогда, когда произведения его противолежащих сторон равны:
Теперь вы знаете какие однокоренные слова подходят к слову Как пишется четырехугольник вместе или раздельно, а так же какой у него корень, приставка, суффикс и окончание. Вы можете дополнить список однокоренных слов к слову "Как пишется четырехугольник вместе или раздельно", предложив свой вариант в комментариях ниже, а также выразить свое несогласие проведенным с морфемным разбором.