Нейросеть с нуля своими руками. Часть 1. Теория
Здравствуйте. Меня зовут Андрей, я frontend-разработчик и я хочу поговорить с вами на такую тему как нейросети. Дело в том, что ML технологии все глубже проникают в нашу жизнь, и о нейросетях сказано и написано уже очень много, но когда я захотел разобраться в этом вопросе, я понял что в интернете есть множество гайдов о том как создать нейросеть и выглядят они примерно следующим образом:
Более подробная информация разбросана кусками по всему интернету. Поэтому я постарался собрать ее воедино и изложить в этой статье. Сразу оговорюсь, что я не являюсь специалистом в области ML или биологии, поэтому местами могу быть не точным. В таком случае буду рад вашим комментариям.
Пока я писал эту статью я понял, что у меня получается довольно объемный лонгрид, поэтому решил разбить ее на несколько частей. В первой части мы поговорим о теории, во второй напишем собственную нейросеть с нуля без использования каких-либо библиотек, в третьей попробуем применить ее на практике.
Так как это моя первая публикация, появляться они будут по мере прохождения модерации, после чего я добавлю ссылки на все части. Итак, приступим.
Для чего нужны нейросети
В нашем глазу есть сенсоры, которые улавливают количество света попадающего через зрачок на заднюю поверхность глаза. Они преобразуют эту информацию в электрические импульсы и передают на прикрепленные к ним нервные окончания. Далее это сигнал проходит по всей нейронной сети, которая принимает решение о том, не опасно ли такое количество света для глаза, достаточно ли оно для того, чтобы четко распознавать визуальную информацию, и нужно ли, исходя из этих факторов, уменьшить или увеличить количество света.
На выходе этой сети находятся мышцы, отвечающие за расширение или сужение зрачка, и приводят эти механизмы в действие в зависимости от сигнала, полученного из нейросети. И таких механизмов огромное количество в теле любого живого существа, обладающего нервной системой.
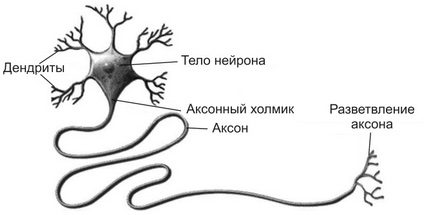
Устройство нейрона
Дендриты нейрона создают дендритное дерево, размер которого зависит от числа контактов с другими нейронами. Это своего рода входные каналы нервной клетки. Именно с их помощью нейрон получает сигналы от других нейронов.
Тело нейрона в природе, достаточно сложная штука, но именно в нем все сигналы, поступившие через дендриты объединяются, обрабатываются, и принимается решение о том передавать ли сигнал далее, и какой силы он должен быть.
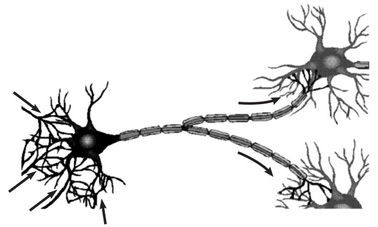
Нейросети в IT
Что же, раз механизм нам понятен, почему бы нам не попробовать воспроизвести его с помощью информационных технологий?
Итак, у нас есть входной слои нейронов, которые, по сути, являются сенсорами нашей системы. Они нужны для того, чтобы получить информацию из окружающей среды и передать ее дальше в нейросеть.
Также у нас есть несколько слоев нейронов, каждый из которых получает информацию от всех нейронов предыдущего слоя, каким-то образом ее обрабатывают, и передают на следующий слой.
И, наконец, у нас есть выходные нейроны. Исходя из сигналов, поступающих от них, мы можем судить о принятом нейросетью решении.
Такой простейший вариант нейронной сети называется перцептрон, и именно его мы с вами и попробуем воссоздать.
Все нейроны по сути одинаковы, и принимают решение о том, какой силы сигнал передать далее с помощью одного и того же алгоритма. Это алгоритм называется активационной функцией. На вход она получает сумму значений входных сигналов, а на выход передает значение выходного сигнала.
Но в таком случае, получается, что все нейроны любого слоя будут получать одинаковый сигнал, и отдавать одинаковое значение. Таким образом мы могли бы заменить всю нашу сеть на один нейрон. Чтобы устранить эту проблему, мы присвоим входу каждого нейрона определенный вес. Этот вес будет обозначать насколько важен для каждого конкретного нейрона сигнал, получаемый от другого нейрона. И тут мы подходим к самому интересному.
То есть мы подаем на вход нейросети определенные данные, для которых мы знаем, каким должен быть результат. Далее мы сравниваем результат, который нам выдала нейросеть с ожидаемым результатом, вычисляем ошибку, и корректируем веса нейронов таким образом, чтобы эту ошибку минимизировать. И повторяем это действие большое количество раз для большого количества наборов входных и выходных данных, чтобы сеть поняла какие сигналы на каком нейроне ей важны больше, а какие меньше. Чем больше и разнообразнее будет набор данных для обучения, тем лучше нейросеть сможет обучиться и впоследствии давать правильный результат. Этот процесс называется обучением с учителем.
Добавим немного математики.
В качестве активационной функции нейрона может выступать любая функция, существующая на всем отрезке значений, получающихся на выходе нейрона и входных данных. Для нашего примера мы возьмем сигмоиду. Она существует на отрезке от минус бесконечности до бесконечности, плавно меняется от 0 до 1 и имеет значение 0,5 в точке 0. Идеальный кандидат. Выглядит она следующим образом:
Таким образом сумма входных значений первого нейрона скрытого слоя будет равна
Передав это значение в активационную функцию, мы получим значение, которое наш нейрон передаст далее по сети в следующий слой.
sigmoid(0,22) = 1 / (1 + e^-0,22) = 0,55
Аналогичные операции произведём для второго нейрона скрытого слоя и получим значение 0,60.
И, наконец, повторим эти операции для единственного нейрона в выходном слое нашей нейросети и получим значение 0,60, что мы условились считать как истину.
Пока что это абсолютно случайное значение, так как веса мы выбирали случайно. Но, предположим, что мы знаем ожидаемое значение для такого набора входных данных и наша сеть ошиблась. В таком случае нам нужно вычислить ошибку и изменить параметры весов, таким образом немного обучив нашу нейросеть.
Первым делом рассчитаем ошибку на выходе сети. Делается это довольно просто, нам просто нужно получить разницу полученного значения и ожидаемого.
Чтобы узнать насколько нам надо изменить веса нашего нейрона, нам нужно величину ошибки умножить на производную от нашей активационной функции в этой точке. К счастью, производная от сигмоиды довольно проста.
Таким образом наша дельта весов будет равна
Новый вес для входа нейрона рассчитывается по формуле
Аналогичным образом рассчитаем новый вес для второго входа выходного нейрона:
Итак, мы скорректировали веса для входов выходного нейрона, но чтобы рассчитать остальные, нам нужно знать ошибку для каждого из нейронов нашей нейросети. Это делается не так очевидно как для выходного нейрона, но тоже довольно просто. Чтобы получить ошибку каждого нейрона нам нужно новый вес нейронной связи умножить на дельту. Таким образом ошибка первого нейрона скрытого слоя равна:
error = 0.18 * 0.24 = 0.04
Теперь, зная ошибку для нейрона, мы можем произвести все те же самые операции, что провели ранее, и скорректировать его веса. Этот процесс называется обратным распространением ошибки.
Итак, мы знаем как работает нейрон, что такое нейронные связи в нейросети и как происходит процесс обучения. Этих знаний достаточно чтобы применить их на практике и написать простейшую нейросеть, чем мы и займемся в следующей части статьи.
Простая нейронка без библиотек и многомерных массивов
Год назад у меня впервые зародилось желание написать свою нейросеть и поэкспериментировать с ней, с тех пор я собирал попадающуюся мне информацию, но до дела у меня дошли руки только сейчас. Я твердо решил написать свою нейросеть с блекджеком, обучением с подкреплением и без сторонних библиотек. Собственно это я и сделал, а так как у меня самого опыта в этом еще не было, я подумал, что это может быть полезно и для других людей, которые хотят в этом разобраться. Хочу сказать, что смысл этой статьи не в правильном способе создания нейросетей, таких статей сотни, а в способе понять, что такое нейросети и наконец перейти к практике. Итак, поехали.
Сначала немного необходимой теории
Почти переходим к практике
Дело в том, что когда я «твердо решил написать свою нейросеть», я совершенно не подумал о том, какую задачу эта нейросеть будет решать, так что это я решил на ходу:
Пишем код
Писать я буду на python, хотя принцип остается тем же и для других языков. Обычно для нейронных сетей используют NumPy с его многомерными массивами, но мне показалось, что для первой нейросети это слишком не наглядно, так что, вдохновившись идеей о создании нейросети методами ООП, я решил реализовать ее через классы. Что я имею ввиду? Я создам класс нейросети и нейрона, а потом уже буду с этим работать. Сначала создаю класс нейрона. У нейрона должны быть 3 переменных: out – выход нейрона, weight – вес синапса, связывающий этот нейрон и родительский, childs – массив дочерних нейронов.
Потом класс сети, в ней нужен только массив выходов. (название Mind я использовал в начале, а потом оно приелось, так что я не стал менять):
Добавляем функции создания:
layers – массив слоев(точнее массив количеств нейронов в слою), не считая выходного
Треть уже готова, осталось сделать функцию активации,
Смысл создавать отдельную функцию, а не просто использовать math.tanh(), в том, чтобы удобнее было ее заменить, в случае, если я решу, что другая будет эффективней.
функции для получения выхода,
Эта функция принимает параметр input – массив входных значений. По сути, эта функция возвращает номер самого активного выходного нейрона или случайного из самых активных. Выход дочернего нейрона возвращается функцией Neuron.getout(input).
и наконец обучение.
На данном этапе мы уже можем запустить нейросеть со случайным входным значением и увидеть, что все работает и нейросеть выдает случайное значение:
Для обучения я реализую альфа-систему подкрепления. Надо оговориться, что у меня считаются «активными связями» все нейроны, модуль выхода которых, больше, либо равен 0.4, а вес синапса может быть отрицательным. Итак, представляю вашему вниманию полный код:
Функции good и bad меняют веса выбранного нейрона на определенное значение с помощью функции Neuron.chweight(). На практике, как следует из названия, good – положительное подкрепление, а bad – отрицательное.
На этом сама нейросеть окончательно закончена, пора приступать к разработке среды обучения. Подробное описание процесса разработки среды не имеет ценности для темы, так что я просто опишу принцип работы:
Таким образом происходит обучение, что наглядно видно на графике, который строится автоматически. График строится на основе значений положительного и отрицательного подкрепления за ход. Рост графика означает преобладание положительного подкрепления над отрицательным.
Итак, первый запуск:
Все работает и даже показывается график, который обновляется каждые 200 ходов.
Я проделывал еще несколько эксспериментов, но их результат совпал с предсказанным, так что они неинтересны.
Заключение
Чуть-чуть обо мне в самом конце:
На самом деле мне 15 и я новичок на Хабре так что, пожалуйста, не сильно ругайтесь на ошибки, это мой первый опыт в написании статей. Если вам понравилось или было полезно, пожалуйста поделитесь этим в комментариях, мне очень важна эта информация. Также если что-то не корректным, прошу обратить мое внимание. Спасибо за прочтение, всего хорошего!
Истинная реализация нейросети с нуля на языке программирования C#
Здравствуй, Хабр! Данная статья предназначена для тех, кто приблизительно шарит в математических принципах работы нейронных сетей и в их сути вообще, поэтому советую ознакомиться с этим перед прочтением. Хоть как-то понять, что происходит можно сначала здесь, потом тут.
Недавно мне пришлось сделать нейросеть для распознавания рукописных цифр(сегодня будет не совсем её код) в рамках школьного проекта, и, естественно, я начал разбираться в этой теме. Посмотрев приблизительно достаточно об этом в интернете, я понял чуть более, чем ничего. Но неожиданно(как это обычно бывает) получилось наткнуться на книгу Саймона Хайкина(не знаю почему раньше не загуглил). И тогда началось потное вкуривание матчасти нейросетей, состоящее из одного матана.
На самом деле, несмотря на обилие математики, она не такая уж и запредельно сложная. Понять сатанистские каракули и письмена этого пособия сможет среднестатистический 11-классник товарищ-физмат или 1
2-курсник технарьского учебного заведения. Помимо этого, пусть книга достаточно объёмная и трудная для восприятия, но вещи, написанные в ней, реально объясняют, что «твориться у тачки под капотом». Как вы поняли я крайне рекомендую(ни в коем случае не рекламирую) «Нейронные сети. Полный курс» Саймона Хайкина к прочтению в том случае, если вам придётся столкнуться с применением/написанием/разработкой нейросетей и прочего подобного stuff’а. Хотя в ней нет материала про новомодные свёрточные сети, никто не мешает загуглить лекции от какого-нибудь харизматичного работника Yandex/Mail.ru/etc. никто не мешает.
Моя видеокарта называется ATI Radeon HD Mobility 4570. И если кто знает, как обратиться к её мощностям для параллелизации нейросетевых вычислений, пожалуйста, напишите в комментарии. Тогда вы поможете мне, и возможно у этой статьи появится продолжение. Не осуждается предложение других ЯП.
Просто, как я понял, она настолько старая, что вообще ничего не поддерживает. Может быть я не прав.
То, что я увидел(третье вообще какая-то эзотерика с некрасивым кодом), несомненно может повергнуть в шок и вас, так как выдаваемое за нейросети связано с ними так же, как и тексты Lil Pump со смыслом. Вскоре я понял, что могу рассчитывать только на себя, и решил написать данную статью, чтобы всякие юзеры не вводили других в заблуждение.
Здесь я не буду рассматривать код сети для распознования цифр(как упоминалось ранее), ибо я оставил его на флэшке, удалив с ноута, а искать сей носитель информации мне лень, и в связи с этим я помогу вам сконструировать многослойный полносвязный персептрон для решения задачи XOR и XAND(XNOR, хз как ещё).
Многослойный полносвязный персептрон.
Один скрытый слой.
4 нейрона в скрытом слое(на этом количестве персептрон сошёлся).
Алгоритм обучения — backpropagation.
Критерий останова — преодоление порогового значения среднеквадратичной ошибки по эпохе.(0.001)
Скорость обучения — 0.1.
Функция активации — логистическая сигмоидальная.

Потом надо осознать, что нам нужно куда-то записывать веса, проводить вычисления, немного дебажить, ну и кортежи поиспользовать. Соответственно, using’и у нас такие.
В папке release||debug этого прожекта располагаются файлы(на каждый слой по одному) по имени типа (fieldname)_memory.xml сами знаете для чего. Они создаются заранее с учётом общего количества весов каждого слоя. Знаю, что XML — это не лучший выбор для парсинга, просто времени было немного на это дело.
Также вычислительные нейроны у нас двух типов: скрытые и выходные. А веса могут считываться или записываться в память. Реализуем сию концепцию двумя перечислениями.
Всё остальное будет происходить внутри пространства имён, которое я назову просто: Neural Network.
Прежде всего, важно понимать, почему нейроны входного слоя я изобразил квадратами. Ответ прост. Они ничего не вычисляют, а лишь улавливают информацию из внешнего мира, то есть получают сигнал, который будет пропущен через сеть. Вследствие этого, входной слой имеет мало общего с остальными слоями. Вот почему стоит вопрос: делать для него отдельный класс или нет? На самом деле, при обработке изображений, видео, звука стоит его сделать, лишь для размещения логики по преобразованию и нормализации этих данных к виду, подаваемому на вход сети. Вот почему я всё-таки напишу класс InputLayer. В нём находиться обучающая выборка организованная необычной структурой. Первый массив в кортеже — это сигналы-комбинации 1 и 0, а второй массив — это пара результатов этих сигналов после проведения операций XOR и XAND(сначала XOR, потом XAND).
Теперь реализуем самое важное, то без чего ни одна нейронная сеть не станет терминатором, а именно — нейрон. Я не буду использовать смещения, потому что просто не хочу. Нейрон будет напоминать модель МакКаллока-Питтса, но иметь другую функцию активации(не пороговую), методы для вычисления градиентов и производных, свой тип и совмещенные линейные и нелинейные преобразователи. Естественно без конструктора уже не обойтись.
Ладно у нас есть нейроны, но их необходимо объединить в слои для вычислений. Возвращаясь к моей схеме выше, хочу объяснить наличие чёрного пунктира. Он разделяет слои так, чтобы показать, что они содержат. То есть один вычислительный слой содержит нейроны и веса для связи с нейронами предыдущего слоя. Нейроны объединяются массивом, а не списком, так как это менее ресурсоёмко. Веса организованы матрицей(двумерным массивом) размера(нетрудно догадаться) [число нейронов текущего слоя X число нейронов предыдущего слоя]. Естественно, слой инициализирует нейроны, иначе словим null reference. При этом эти слои очень похожи друг на друга, но имеют различия в логике, поэтому скрытые и выходной слои должны быть реализованы наследниками одного базового класса, который кстати оказывается абстрактным.
Класс Layer — это абстрактный класс, поэтому нельзя создавать его экземпляры. Это значит, что наше желание сохранить свойства «слоя» выполняется путём наследования родительского конструктора через ключевое слово base и пустой конструктор наследника в одну строчку(ибо вся логика конструктора определена в базовом классе, и её не надо переписывать).
Теперь непосредственно классы-наследники: Hidden и Output. Сразу два класса в цельном куске кода.
В принципе, всё самое важное я описал в комментариях. У нас есть все компоненты: обучающие и тестовые данные, вычислительные элементы, их «конгламераты». Теперь настало время всё связать обучением. Алгоритм обучения — backpropagation, следовательно критерий останова выбираю я, и выбор мой — есть преодоление порогового значения среднеквадратичной ошибки по эпохе, которое я выбрал равным 0.001. Для поставленной цели я написал класс Network, описывающий состояние сети, которое принимается в качестве параметра многих методов, как вы могли заметить.
Результат обучения.
Итого, путём насилования мозга несложных манипуляций, мы получили основу работающей нейронной сети. Для того, чтобы заставить её делать что-либо другое, достаточно поменять класс InputLayer и подобрать параметры сети для новой задачи.
За сим всё, буду рад ответить на вопросы в комментариях, а пока извольте, новые дела ждут.
P.S.: Для желающих потыкать в код клацать.
UPD1(22.10.2020): господи как давно это было, надеюсь больше не буду писать такие статьи. Скорее всего в то время хотел поделиться с сообществом таким кодом, но так в ML никто не пишет)
Как построить свою первую нейросеть
С помощью статьи PhD Оксфордского университета и автора книг о глубоком обучении Эндрю Траска показываем, как написать простую нейронную сеть на Python. Она умещается всего в девять строчек кода и выглядит вот так:
from numpy import exp, array, random, dot
training_set_inputs = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]])
training_set_outputs = array([[0, 1, 1, 0]]).T
random.seed(1)
synaptic_weights = 2 * random.random((3, 1)) — 1
for iteration in xrange(10000):
output = 1 / (1 + exp(-(dot(training_set_inputs, synaptic_weights))))
synaptic_weights += dot(training_set_inputs.T, (training_set_outputs — output) * output * (1 — output))
print 1 / (1 + exp(-(dot(array([1, 0, 0]), synaptic_weights))))
Чуть ниже объясним как получается этот код и какой дополнительный код нужен к нему, чтобы нейросеть работала. Но сначала небольшое отступление о нейросетях и их устройстве.
Человеческий мозг состоит из ста миллиардов клеток, которые называются нейронами. Они соединены между собой синапсами. Если через синапсы к нейрону придет достаточное количество нервных импульсов, этот нейрон сработает и передаст нервный импульс дальше. Этот процесс лежит в основе нашего мышления.
Мы можем смоделировать это явление, создав нейронную сеть с помощью компьютера. Нам не нужно воссоздавать все сложные биологические процессы, которые происходят в человеческом мозге на молекулярном уровне, нам достаточно знать, что происходит на более высоких уровнях.
Для этого мы используем математический инструмент — матрицы, которые представляют собой таблицы чисел. Чтобы сделать все как можно проще, мы смоделируем только один нейрон, к которому поступает входная информация из трех источников и есть только один выход (рис. 1). Наша задача — научить нейронную сеть решать задачу, которая изображена на рисунке ниже. Первые четыре примера будут нашим тренировочным набором. Получилось ли у вас увидеть закономерность? Что должно быть на месте вопросительного знака — 0 или 1?
Вы могли заметить, что вывод всегда равен значению левого столбца. Так что ответом будет 1.
Процесс тренировки
Но как научить наш нейрон правильно отвечать на заданный вопрос? Для этого мы зададим каждому входящему сигналу вес, который может быть положительным или отрицательным числом. Если на входе будет сигнал с большим положительным весом или отрицательным весом, то это сильно повлияет на решение нейрона, которое он подаст на выход. Прежде чем мы начнем обучение модели, зададим для каждого примера случайное число в качестве веса. После этого мы можем приняться за тренировочный процесс, который будет выглядеть следующим образом:
В какой-то момент веса достигнут оптимальных значений для тренировочного набора. Если после этого нейрону будет дана новая задача, которая следует такой же закономерности, он должен дать верный ответ.
Формула для вычисления выхода нейронной сети
Итак, что же из себя представляет формула, которая рассчитывает значение выхода нейрона? Для начала мы возьмем взвешенную сумму входных сигналов:
После этого мы нормализуем это выражение, чтобы результат был между 0 и 1. Для этого, в этом примере, я использую математическую функцию, которая называется сигмоидой:
Если мы нарисуем график этой функции, то он будет выглядеть как кривая в форме буквы S (рис. 4).
Подставив первое уравнения во второе, мы получим итоговую формулу выхода нейрона.
Вы можете заметить, что для простоты мы не задаем никаких ограничений на входящие данные, предполагая, что входящий сигнал всегда достаточен для того, чтобы наш нейрон подал сигнал на выход.
Машинное обучение и нейросети
Комплект продвинутых курсов для освоения машинного и глубокого обучения от классических моделей до нейронных сетей. Дополнительная скидка 5% по промокоду BLOG.
Формула корректировки весов
Во время тренировочного цикла (он изображен на рисунке 3) мы постоянно корректируем веса. Но на сколько? Для того, чтобы вычислить это, мы воспользуемся следующей формулой:
Давайте поймем почему формула имеет такой вид. Сначала нам нужно учесть то, что мы хотим скорректировать вес пропорционально размеру ошибки. Далее ошибка умножается на значение, поданное на вход нейрона, что, в нашем случае, 0 или 1. Если на вход был подан 0, то вес не корректируется. И в конце выражение умножается на градиент сигмоиды. Разберемся в последнем шаге по порядку:
Градиент сигмоиды может быть найден по следующей формуле:
Таким образом, подставляя второе уравнение в первое, конечная формула для корректировки весов будет выглядеть следующим образом:
Существуют и другие формулы, которые позволяют нейрону обучаться быстрее, но преимущество этой формулы в том, что она достаточно проста для понимания.
Как написать это на Python
Хотя мы не будем использовать специальные библиотеки для нейронных сетей, мы импортируем следующие 4 метода из математической библиотеки numpy:
Теперь мы можем, например, представить наш тренировочный набор с использованием array():
training_set_inputs = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]])=
training_set_outputs = array([[0, 1, 1, 0]]).T
Теперь мы готовы к более изящной версии кода. После нее добавим несколько финальных замечаний.
Обратите внимание, что на каждой итерации мы обрабатываем весь тренировочный набор одновременно. Таким образом наши переменные все являются матрицами.
Итак, вот полноценно работающий пример нейронной сети, написанный на Python:
from numpy import exp, array, random, dot
class NeuralNetwork():
def __init__(self):
Задаем порождающий элемент для генератора случайных чисел, чтобы он генерировал одинаковые числа при каждом запуске программы
random.seed(1)
Функция сигмоиды, график которой имеет форму буквы S.
Мы используем эту функцию, чтобы нормализовать взвешенную сумму входных сигналов.
def __sigmoid(self, x):
return 1 / (1 + exp(-x))
Производная от функции сигмоиды. Это градиент ее кривой. Его значение указывает насколько нейронная сеть уверена в правильности существующего веса.
def __sigmoid_derivative(self, x):
return x * (1 — x)
Мы тренируем нейронную сеть методом проб и ошибок, каждый раз корректируя вес синапсов.
def train(self, training_set_inputs, training_set_outputs, number_of_training_iterations):
for iteration in xrange(number_of_training_iterations):
Тренировочный набор передается нейронной сети (одному нейрону в нашем случае).
output = self.think(training_set_inputs)
Вычисляем ошибку (разницу между желаемым выходом и выходом, предсказанным нейроном).
error = training_set_outputs — output
Умножаем ошибку на входной сигнал и на градиент сигмоиды. В результате этого, те веса, в которых нейрон не уверен, будут откорректированы сильнее. Входные сигналы, которые равны нулю, не приводят к изменению веса.
adjustment = dot(training_set_inputs.T, error * self.__sigmoid_derivative(output))
Корректируем веса.
self.synaptic_weights += adjustment
Заставляем наш нейрон подумать.
def think(self, inputs):
Пропускаем входящие данные через нейрон.
return self.__sigmoid(dot(inputs, self.synaptic_weights))
if __name__ == «__main__»:
Инициализируем нейронную сеть, состоящую из одного нейрона.
neural_network = NeuralNetwork()
print «Random starting synaptic weights:
» print neural_network.synaptic_weights
Тренировочный набор для обучения. У нас это 4 примера, состоящих из 3 входящих значений и 1 выходящего значения.
training_set_inputs = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]])
training_set_outputs = array([[0, 1, 1, 0]]).T
Обучаем нейронную сеть на тренировочном наборе, повторяя процесс 10000 раз, каждый раз корректируя веса.
neural_network.train(training_set_inputs, training_set_outputs, 10000)
print «New synaptic weights after training:
» print neural_network.synaptic_weights
Этот код также можно найти на GitHub. Обратите внимание, что если вы используете Python 3, то вам будет нужно заменить команду “xrange” на “range”.
Несколько финальных замечаний
Попробуйте теперь запустить нейронную сеть, используя в терминале эту команду:
Результат должен быть таким:
Random starting synaptic weights:
[[-0.16595599]
[ 0.44064899]
[-0.99977125]]
New synaptic weights after training:
[[ 9.67299303]
[-0.2078435 ]
[-4.62963669]]
Ура, мы построили простую нейронную сеть с помощью Python!
Сначала нейронная сеть задала себе случайные веса, затем обучилась на тренировочном наборе. После этого она предсказала в качестве ответа 0.99993704 для нового примера [1, 0, 0]. Верный ответ был 1, так что это очень близко к правде!
Традиционные компьютерные программы обычно не способны обучаться. И это то, что делает нейронные сети таким поразительным инструментом: они способны учиться, адаптироваться и реагировать на новые обстоятельства. Точно так же, как и человеческий мозг.
Конечно, мы создали модель всего лишь одного нейрона для решения очень простой задачи. Но что если мы соединим миллионы нейронов? Сможем ли мы таким образом однажды воссоздать реальное сознание?
Машинное обучение и нейросети
Научим вас создавать чат-ботов, нейросети и агента для игры в Pong.