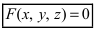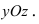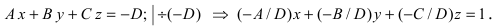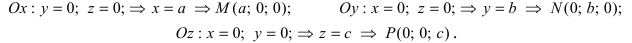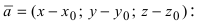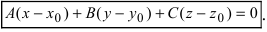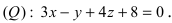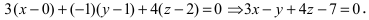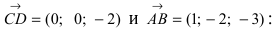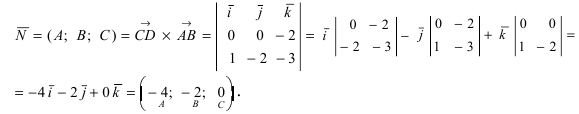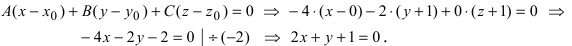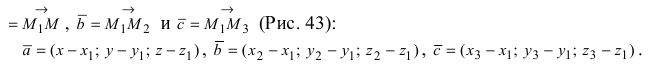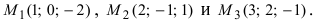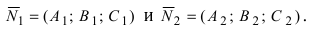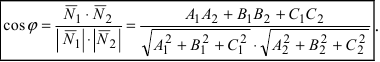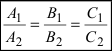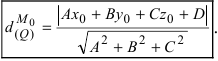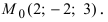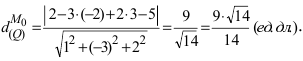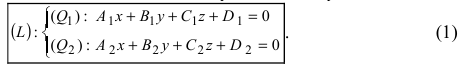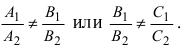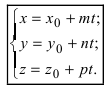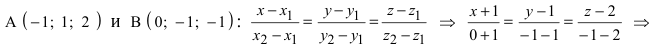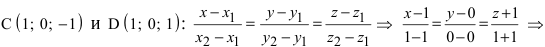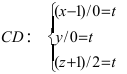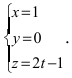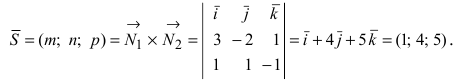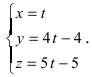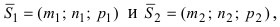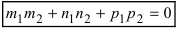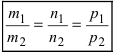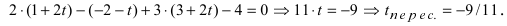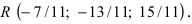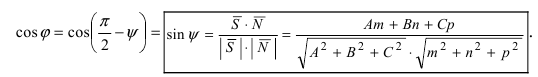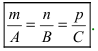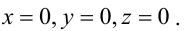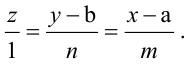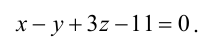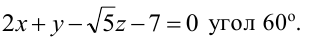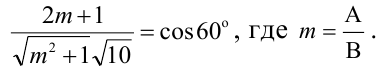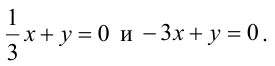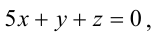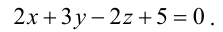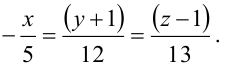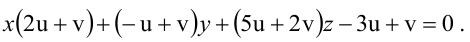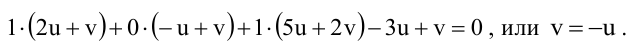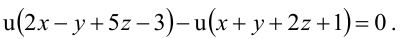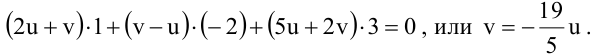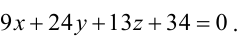Плоскость и прямая в пространстве с примерами решения
Содержание:
Плоскость в пространстве
Общее уравнение плоскости
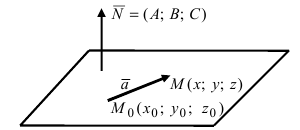
Определение: Уравнение вида
Определение: Порядок поверхности определяется по высшему показателю степени переменных х, у и z или по сумме показателей степени в произведении этих величин.
Определение: Уравнение вида Ax+By+Cz+D=O называется общим уравнением плоскости.
Рассмотрим частные случаи приведенного уравнения:
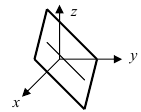
1. D = 0; Ах + By + Сz = 0. Из этого уравнения видно, что точка О(0; 0; 0) удов- летворяет этому уравнению, следовательно, это уравнение описывает плоскость, проходящую через начало координат (Рис. 36).
Рис. 36. Плоскость, проходящая через начало координат.
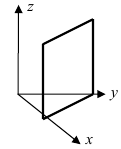
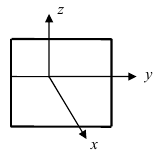
2. С = 0; Ах + Ву + D = 0. Этому уравнению удовлетворяет любое значение переменной z, поэтому данное уравнение описывает плоскость, которая параллельна оси аппликат (Oz) (Рис. 37).
Рис. 37. Плоскость, проходящая параллельно оси аппликат.
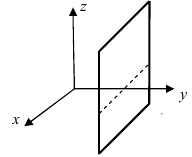
Замечание: При отсутствии в уравнении плоскости одной из переменных величин говорит о том, что плоскость параллельна соответствующей координатной оси.
Рис. 38. Плоскость, проходящая через начало координат параллельно оси аппликат.
4. 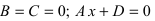
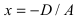
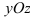
Рис. 39. Плоскость, проходящая параллельно координатной плоскости
Рис. 40. Координатная плоскость 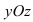
Другие уравнения плоскости
1. Уравнение плоскости в отрезках. Пусть в уравнении 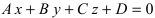
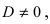
Введем следующие обозначения 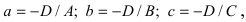
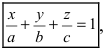
Откладывая на координатных осях точки М, N и Р, соединяя их прямыми лучим изображение данной плоскости (для определенности принято, что параметры а, b, с положительные) (Рис. 41):
Рис. 41. Отрезки, отсекаемые плоскостью на координатных осях.
Из рисунка видно, что числа а, b, с показывают отрезки, отсекаемые плоскостью на координатных осях, считая от начала координат.
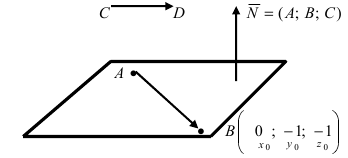
2. Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданному вектору. Пусть задана точка 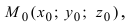
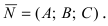
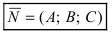
Возьмем на плоскости произвольную точку 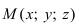
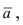
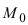
Рис. 42. Плоскость, проходящая через заданную точку перпендикулярно к нормальному вектору.
В силу того, вектор 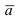
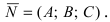
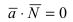
Пример:
Составить уравнение плоскости, проходящей через т. 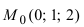
Решение:
Так как искомая плоскость параллельна плоскости (Q), то нормальный вектор этой плоскости 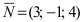
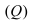
Пример:
Решение:
Построим на искомой плоскости вектор 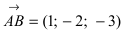
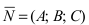
Уравнение плоскости, проходящей через заданную точку 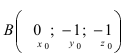
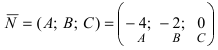
Отметим, что при выборе точки, через которую проходит искомая плоскость из точек 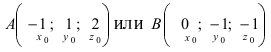
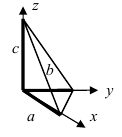
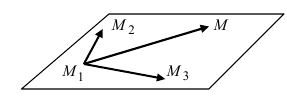
3. Уравнение плоскости, проходящей через три заданные точки. Пусть плоскость проходит через 3 известные точки 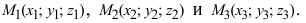
Рис. 43. Плоскость, проходящая через три заданные точки.
Вектора 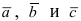
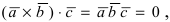
Замечание: Полученный определитель третьего порядка раскрывается по элементам первой строки.
Пример:
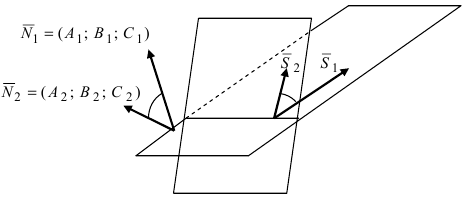
Составить уравнение плоскости, проходящей через три заданные точки
Решение:
Основные задачи о плоскости в пространстве
1. Угол между пересекающимися плоскостями. Пусть даны две пересекающиеся плоскости 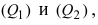
Пусть линия пересечения плоскостей определяется прямой (l). Из одной точки этой прямой проведем два перпендикулярных к прямой вектора 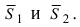
Рис.44. Угол между плоскостями.
В силу того, что 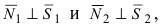
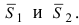
Следствие: Если плоскости перпендикулярны (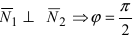
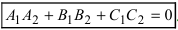
Следствие: Если плоскости параллельны, то нормальные вектора коллинеарны, следовательно, условие параллельности плоскостей:
2. Расстояние от данной точки до заданной плоскости. Расстояние от данной точки 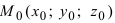
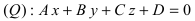
Пример:
На каком расстоянии от плоскости 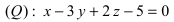
Решение:
Воспользуемся приведенной формулой:
Прямая в пространстве
Общее уравнение прямой
Прямая в пространстве может быть задана как пересечение двух плоскостей:
Определение: Геометрическое место точек пространства, удовлетворяющих системе уравнений (1), называется прямой в пространстве, а система уравнений (1) называется общим уравнением прямой.
Замечание: Для того чтобы система уравнений (1) определяла прямую в пространстве необходимо и достаточно, чтобы нормальные вектора плоскостей, определяющих прямую, 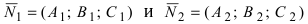
Пусть прямая проходит через точку 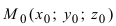
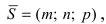
Замечание: Если в уравнении (2) одна из проекций направляющего вектора равна 0, то это означает, что прямая перпендикулярна соответствующей координатной оси.
Пример:
Как расположена прямая 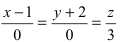
Решение:
Согласно замечанию эта прямая будет перпендикулярна осям абсцисс и ординат (параллельна оси аппликат) и будет проходить через точку 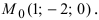
Пример:
Записать уравнение прямой 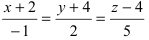
Решение:
Приравняем каждую дробь к параметру t: 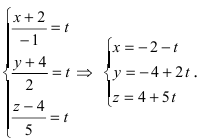
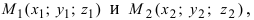
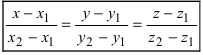
Пример:
Решение:
Составим каноническое уравнение прямой линии, проходящей через точки
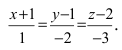
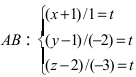
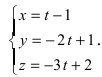
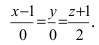
Основные задачи о прямой в пространстве
1. Переход от общего уравнения прямой к каноническому. Пусть прямая задана общим уравнением 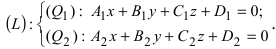
Пример:
Записать уравнение прямой 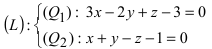
Решение:
Запишем каноническое 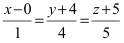
Угол между пересекающимися прямыми
Угол между двумя пересекающимися прямыми определяется как угол между их направляющими векторами. Если прямые 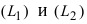
соответственно, то угол между прямыми определяется по формуле:
Следствие: Если прямые перпендикулярны (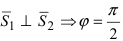
Следствие: Если прямые параллельны, то направляющие вектора коллинеарны, следовательно, условие параллельности прямых:
Координаты точки пересечения прямой и плоскости
Пусть прямая (L) задана общим уравнением 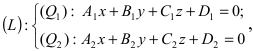
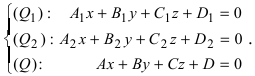
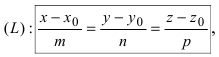
Рассмотрим возможные случаи:
Пример:
Найти координаты точки пересечения прямой (L), заданной уравнением 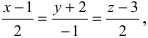
Решение:
Перепишем уравнение прямой (L) в параметрическом виде 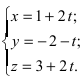
Найденное значение параметра 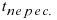
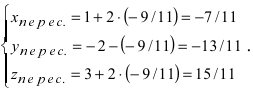
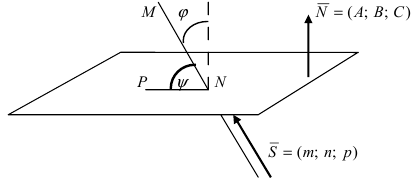
Угол между прямой и плоскостью
Пусть дана плоскость (Q) с нормальным вектором 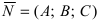
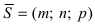
Рис. 45. Угол между прямой и плоскостью.
Угол 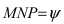
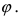
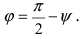
Следствие: Если прямая перпендикулярна плоскости (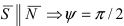
Следствие: Если прямая параллельна плоскости (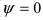
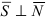
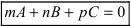
Плоскость и прямая в пространстве
Всякое уравнение первой степени относительно координат 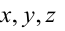

Вектор 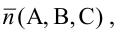
Особые случаи уравнения (3.1):
Уравнения координатных плоскостей:
Прямая в пространстве может быть задана:
Тогда прямая определяется уравнениями:
Уравнения (3.4) называются каноническими уравнениями прямой.
Вектор 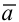
Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t: 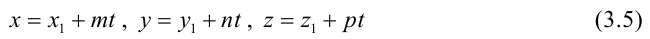
От уравнений (3.6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:
От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор 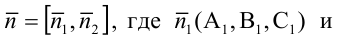
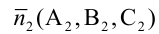
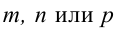
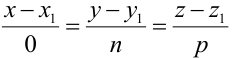
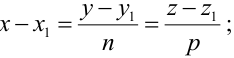
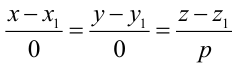
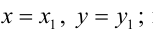
Пример:
Составьте уравнение плоскости, зная, что точка А(1,-1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.
Решение:
По условию задачи вектор 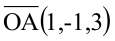
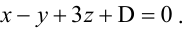
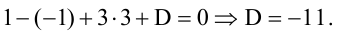
Пример:
Составьте уравнение плоскости, проходящей через ось Oz и образующей с плоскостью
Решение:
Плоскость, проходящая через ось Oz, задается уравнением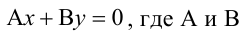
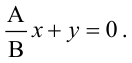
Решая квадратное уравнение 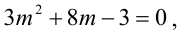
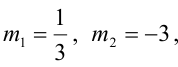
Пример:
Составьте канонические уравнения прямой:
Решение:
Канонические уравнения прямой имеют вид:
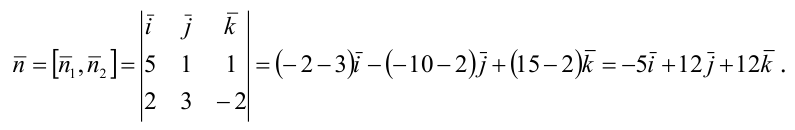
Пример:
В пучке, определяемом плоскостями 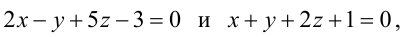
Решение:
Уравнение пучка, определяемого данными плоскостями, имеет вид 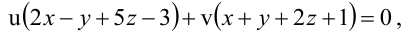
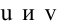
Для того, чтобы из пучка выделить плоскость, проходящую через точку М, подставим координаты точки М в уравнение пучка. Получим:
Тогда уравнение плоскости, содержащей М, найдем, подставив 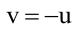
Т.к. и 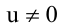
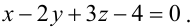
Значит, уравнение второй плоскости имеет вид: 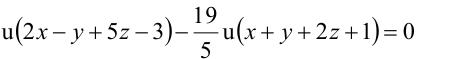
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.