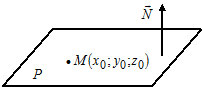Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через данную точку и перпендикуляной данной прямой. Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямой (канонический или параметрический) введите координаты точки и коэффициенты уравнения прямой в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой − теория, примеры и решения
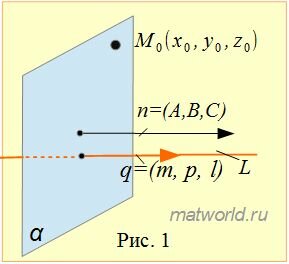
Построить уравнение плоскости α, проходящей через точку M0 и перпендинулярной прямой L.
 |
Решение. Уравнение плоскости, проходящей через точку M0 и имеющий нормальный вектор n=<A, B, C> имеет следующий вид:
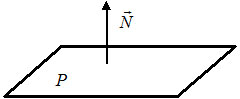
Направляющий вектор прямой L имеет вид q=<m, p, l>. Поскольку прямая L и плоскость α перпендикулярны друг другу, следовательно нормальный вектор плоскостти и направляющий вектор прямой должны быть коллинеарны (Рис.1). Тогда вместо координат нормального вектора плоскости нужно подставить координаты направляющего вектора прямой L. Получим следующее уравнение плоскости:
Упростим уравнение (3):
Таким образом уравнение (4) определяет плоскость, проходящей через точку M0(x0, y0, z0) и перпендикулярной прямой (1).
Ответ. Уравнение плоскости прпоходящей через точку M0(x0, y0, z0) и перпендикулярной прямой (1) имеет вид (4).
Пример 1. Найти уравнение плоскости α, проходящую через точку M0(3, −1, 2) и перпендикулярной прямой L:
Решение. Уравнение плоскости α, проходящей через точку M0(x0, y0, z0) и имеющий нормальный вектор n=<A, B, C> представляется формулой (2).
Направляющий вектор прямой L имеет следующий вид: :
Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.е. уравнение плоскости (2) примет следующий вид:
Подставляя координаты точки M0 и направляющего вектора q в (8), получим:
Упростим уравнение (9):
Ответ: Уравнение плоскости, проходящей через точку M0(3, −1, 2) и перпендикулярной прямой (7) имеет вид (10).
Пример 2. Найти уравнение плоскости α, проходящую через точку M0(4, 3, −6) и перпендикулярной прямой L, заданной параметрическим уравнением:
Решение. Приведем параметрическое уравнение (11) к каноническому виду:
Уравнение плоскости α, проходящей через точку M0(x0, y0, z0) и имеющий нормальный вектор n=<A, B, C> представляется формулой:
Направляющий вектор прямой L имеет следующий вид:
Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.е. уравнение плоскости (12) примет следующий вид:
Подставляя координаты точки M0 и направляющего вектора q в (13), получим:
 |
Упростим уравнение (13):
Ответ. Уравнение плоскости, проходящей через точку M0(4, 3, −6) и перпендикулярной прямой (11) имеет вид (14).
Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.
В этой статье мы поговорим о том, как составляется уравнение плоскости, проходящей через заданную точку трехмерного пространства перпендикулярно к заданной прямой. Сначала разберем принцип нахождения уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой, после чего подробно разберем решения характерных примеров и задач.
Навигация по странице.
Нахождение уравнения плоскости, проходящей через заданную точку пространства перпендикулярно к заданной прямой.
Поставим перед собой следующую задачу.
Сначала вспомним один важный факт.
Теперь покажем, как находится уравнение этой единственной плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.
Мы можем написать общее уравнение плоскости, если нам известны координаты точки, лежащей в этой плоскости, и координаты нормального вектора плоскости.
Итак, получаем алгоритм для нахождения уравнения плоскости 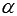
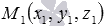
Из найденного общего уравнения плоскости вида 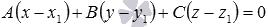
Примеры составления уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.
Рассмотрим решения нескольких примеров, в которых находится уравнение плоскости, проходящей через заданную точку пространства перпендикулярно к заданной прямой.
Уравнение плоскости, проходящей через точку и прямую онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через данную точку и через данную прямую (точка не лежит на этой прямой). Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямой (канонический или параметрический) введите координаты точки и коэффициенты уравнения прямой в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Уравнение плоскости, проходящей через точку и прямую − теория, примеры и решения
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L:
Задача заключается в построении уравнения плоскости α, проходящей через точку M0 и и через прямую L(Рис.1).
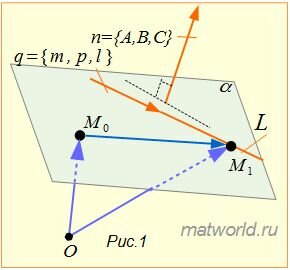 |
Решение. Уравнение плоскости, проходящей через точку M0 и имеющий нормальный вектор n=<A, B, C> имеет следующий вид:
Направляющий вектор прямой L имеет вид q=<m, p, l>. Поскольку плоскость проходит через прямую L, то она проходит также через точку M1(x1, y1, z1). Тогда уравнение плоскости, проходящей через точку M1(x1, y1, z1) имеет вид:
Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q прямой L, т.е. скалярное произведение этих векторов должен быть равным нулю:
Вычитая уравнение (3) из уравнения (2), получим:
Решая совместно уравнения (4) и (5) отностительно коэффициентов A, B, C получим такие значения A, B, C, при которых уравнение (2) проходит через точку M0 и через прямую (1). Для решения систему уравнений (4), (5), запишем их в матричном виде:
Как решить систему линейных уравнений посмотрите на странице метод Гаусса онлайн.
Получив частное решение уравнения (6) и подставив полученные значения A, B, C в (2), получим решение задачи.
Решение. Уравнение плоскости α, проходящей через точку M0(x0, y0, z0)=M0(1, 2, 5) и имеющий нормальный вектор n=<A, B, C> представляется формулой (2).
Вычитая уравнение (3) из уравнения (2), получим:
Направляющий вектор прямой L имеет следующий вид:
Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q прямой L, т.е. скалярное произведение этих векторов должен быть равным нулю:
Решим систему линейных уравнений (10) и (11) отностительно A, B, C. Для этого представим эти уравнения в матричном виде:
Решив однородную систему линейных уравнений (12) используя метод Гаусса, найдем следующее частное решение:
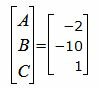 |
Подставляя значения коэффициентов A, B, C в уравнение плоскости (2), получим:
Упростим уравнение (13):
Ответ: Уравнение плоскости, проходящей через точку M0(1, 2, 5) и через прямую (7) имеет вид (14).
Пример 2. Найти уравнение плоскости α, проходящую через точку M0(4, 3, −6) и через прямую L, заданной параметрическим уравнением:
Решение. Приведем параметрическое уравнение (15) к каноническому виду:
Уравнение плоскости α, проходящей через точку M0(x0, y0, z0) и имеющий нормальный вектор n=<A, B, C> представляется формулой:
Поскольку плоскость проходит через прямую L, то она проходит также через точку M1(x1, y1, z1)=(0, 2, 4). Тогда уравнение плоскости, проходящей через точку M1(x1, y1, z1) имеет вид:
Вычитая уравнение (18) из уравнения (17), получим:
Направляющий вектор прямой L имеет следующий вид:
Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n должен быть ортогональным направляющему вектору прямой L :
Решим систему линейных уравнений (21) и (22) отностительно A, B, C. Для этого представим эти уравнения в матричном виде:
Решив однородную систему линейных уравнений (23) используя метод Гаусса, найдем следующее частное решение:
 |
Подставляя значения коэффициентов A, B, C в уравнение плоскости (17), получим:
Упростим уравнение (24):
Уравнение плоскости можно представить более упрощенном виде, умножив на число 23.
Ответ: Уравнение плоскости, проходящей через точку M0(4, 3, −6) и через прямую (16) имеет вид (26).
Математический портал
Nav view search
Navigation
Search
Плоскость в пространстве, всевозможные уравнения, расстояние от точки до плоскости.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Существуют такие формы записи уравнения плоскости:
Примеры:
2.180.
Решение.
2.181.
Решение.
2.182.
Решение.
2.183.
Решение.
$(x-1)(-1)1+1\cdot z\cdot 0+(y-2)3-3(-1)z-0\cdot 1\cdot(x-1)-1(y-2)1=0\Rightarrow$
2.184.
Решение.
Воспользуемся формулой (4):
Уравнение плоскости через координаты вектора нормали и точки: онлайн-калькулятор
Плоскость — это бесконечная поверхность с принадлежащими ей прямыми, через которые проходят любые две ее точки. Нормалью к кривой в указанной точке является прямая, расположенная перпендикулярно к касательной прямой в заданной точке кривой.
Чтобы найти уравнение плоскости, перпендикулярной вектору онлайн, необходимо:
Как найти уравнение плоскости через координаты вектора нормали и точки с помощью онлайн-калькулятора
Рассмотрим пример, наглядно демонстрирующий работу с онлайн-калькулятором. Пусть нужно найти уравнение плоскости по вектору нормали к ней и координатам точки, лежащей в плоскости. Для этого в онлайн-калькуляторе просто зададим известную точку и соответствующий вектор (нормаль):
Впишем значения в пустые поля и нажмем «Рассчитать» (значения взяты произвольно):
После этого калькулятор автоматически выдаст подробное решение с ответом:
Материалы, которые помогут вам лучше разобраться в теме:
Уравнение плоскости через точку перпендикулярно вектору онлайн
Сервис предназначен для геометрических вычислений, которыми пользуются учащиеся школ и студенты университетов для подготовки к занятиям.
Решение задачи с помощью онлайн-калькулятора имеет преимущества:
Пошаговые вычисления позволяют учащемуся вникнуть в процесс решения задачи по геометрии и справляться с заданиями самостоятельно. Подготовка к занятиям благодаря калькулятору занимает меньше времени и происходит более продуктивно.