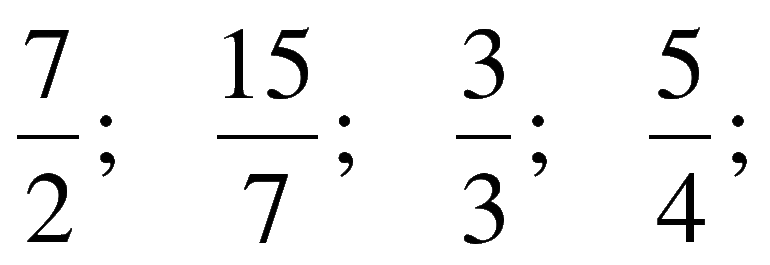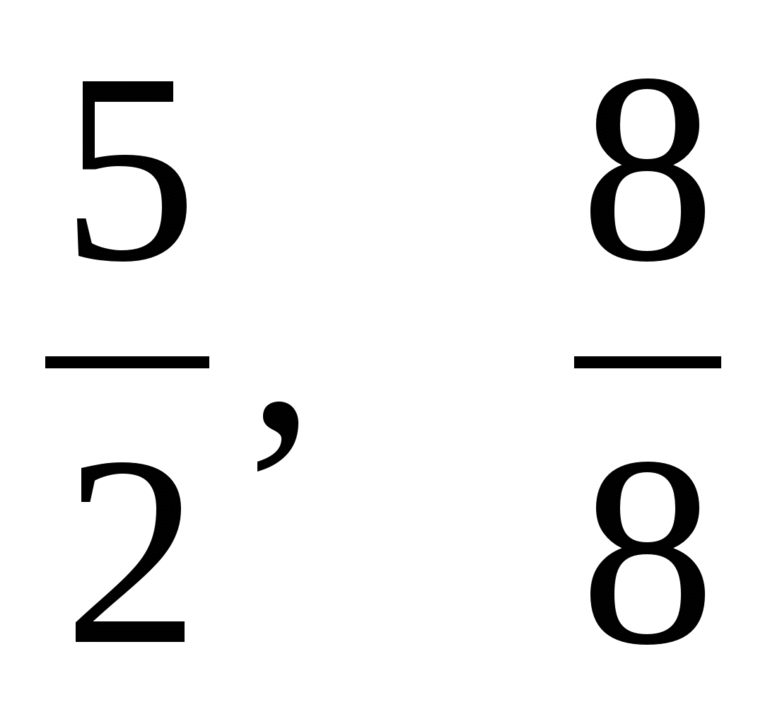дробно-рациональный
Смотреть что такое «дробно-рациональный» в других словарях:
Цифровой фильтр — Цифровой фильтр в электронике любой фильтр, обрабатывающий цифровой сигнал с целью выделения и/или подавления определённых частот этого сигнала. В отличие от цифрового, аналоговый фильтр имеет дело с аналоговым сигналом, его свойства… … Википедия
Фильтр с бесконечной импульсной характеристикой — (Рекурсивный фильтр, БИХ фильтр) или IIR фильтр (IIR сокр. от infinite impulse response бесконечная импульсная характеристика) линейный электронный фильтр, использующий один или более своих выходов в качестве входа, то есть… … Википедия
Дискретный фильтр — Цифровой фильтр в электронике любой фильтр, обрабатывающий цифровой сигнал с целью выделения и/или подавления определённых частот этого сигнала. В отличие от цифрового аналоговый фильтр имеет дело с аналоговым сигналом, его свойства недискретны,… … Википедия
Рекурсивный фильтр — Фильтр с бесконечной импульсной характеристикой (Рекурсивный фильтр, БИХ фильтр) линейный электронный фильтр, использующий один или более своих выходов в качестве входа, то есть образует обратную связь. Основным свойством таких фильтров является … Википедия
Теорема Рауса — Гурвица — Теорема Рауса Гурвица предоставляет возможность определить, является ли данный многочлен устойчивым по Гурвицу. Была доказана в 1895 году и названа в честь Эдварда Джона Рауса (англ.) и Адольфа Гурвица. Содержание 1 Условные… … Википедия
математическое деление — ▲ алгебраическая функция ↑ обратный, фактор < > умножение деление функция, находящаяся в обратном соответствии от аргумента; операция, обратная умножению; нахождение кратной величины; если величина является произведением двух других… … Идеографический словарь русского языка
Синдром хронической передозировки инсулина — Michael Somogyi (1883 1971) Синдром хронической передозировки инсулина (СХПИ, феномен (синдром) Сомоджи, рикошетная гипергликемия, постгипогликемическая гиперглик … Википедия
Теорема Рауса — Теорема Рауса Гурвица предоставляет возможность определить, является ли данный многочлен устойчивым по Гурвицу. Была доказана в 1895 году и названа в честь Эдварда Джона Рауса (англ.) и Адольфа Гурвица. Содержание 1 Условные… … Википедия
Дробно-рациональные уравнения
Что такое дробно-рациональные уравнения
Дробно-рациональными уравнениями называют такие выражения, которые представляется возможным записать, как:
при P ( x ) и Q ( x ) в виде выражений, содержащих переменную.
Таким образом, дробно-рациональные уравнения обязательно содержат как минимум одну дробь с переменной в знаменателе с любым модулем.
1 2 x + x x + 1 = 1 2
Уравнения, которые не являются дробно-рациональными:
Как решаются дробно-рациональные уравнения
В процессе решения дробно-рациональных уравнений обязательным действием является определение области допустимых значений. Найденные корни следует проверить на допустимость, чтобы исключить посторонние решения.
Алгоритм действий при стандартном способе решения:
Разберем предложенный алгоритм на практическом примере. Предположим, что имеется дробно-рациональное уравнение, которое требуется решить:
Начать следует с области допустимых значений:
Воспользуемся правилом сокращенного умножения:
В результате общим знаменателем дробей является:
Выполним умножение каждого из членов выражения на общий знаменатель:
После сокращения избавимся от скобок и приведем подобные слагаемые:
Осталось решить квадратное уравнение:
Согласно ОДЗ, первый корень является лишним, так как не удовлетворяет условию, по которому корень не равен 2. Тогда в ответе можно записать:
Примеры задач с ответами для 9 класса
Требуется решить дробно-рациональное уравнение:
Определим область допустимых значений:
Квадратный трехчлен x 2 + 7 x + 10 следует разложить на множители, руководствуясь формулой:
Сократим дроби, избавимся от скобок, приведем подобные слагаемые:
Потребуется решить квадратное уравнение:
Первый корень не удовлетворяет условиям ОДЗ, поэтому в ответ нужно записать только второй корень.
Дано дробно-рациональное уравнение, корни которого требуется найти:
В первую очередь следует переместить все слагаемые влево и привести дроби к минимальному единому знаменателю:
Заметим, что получилось нулевое значение для дроби. Известно, что дробь может равняться нулю, если в числителе нуль, а знаменатель не равен нулю. На основании этого можно составить систему:
Следует определить такие значения для переменной, при которых в дроби знаменатель будет обращаться в нуль. Такие значения необходимо удалить из ОДЗ:
Далее можно определить значения для переменных, которые при подстановке в уравнение обращают числитель в нуль:
Получилось квадратное уравнение, которое можно решить:
Сравнив корни с условиями области допустимых значений, можно сделать вывод, что оба корня являются решениями данного уравнения.
Нужно решить дробно-рациональное уравнение:
На первом шаге следует перенести все слагаемые в одну сторону и привести дроби к минимальному единому знаменателю:
Перечисленные значения переменной обращают знаменатель в нуль. По этой причине их необходимо удалить из области допустимых значений.
Корни квадратного уравнения:
Заметим, что второй корень не соответствует ОДЗ. Таким образом, в ответе остается только первый корень.
Найти корни уравнения:
Согласно стандартному алгоритму решения дробно-рациональных уравнений, выполним перенос всех слагаемых в одну сторону. Далее необходимо привести к дроби к наименьшему общему знаменателю:
Такое значение переменной, при котором знаменатель становится равным нулю, нужно исключить из области допустимых значений:
Заметим, что это частный случай линейного уравнения, которое обладает бесконечным множеством корней. При подстановке какого-либо числа на место переменной х в любом случае числовое равенство будет справедливым. Единственным недопустимым значением для х в данном задании является число 3, которое не входит в ОДЗ.
Ответ: х — любое число, за исключением 3.
Требуется вычислить корни дробно-рационального уравнения:
На первом этапе необходимо выполнить перенос всех слагаемых влево, привести дроби к минимальному единому знаменателю:
Данные значения переменной х являются недопустимыми, так как в этом случае теряется смысл дроби в связи с тем, что знаменатель принимает нулевое значение.
Заметим, что 2 не входит в область допустимых значений. В связи с этим, можно заключить, что у уравнения отсутствуют корни.
Ответ: корни отсутствуют
Нужно найти корни уравнения:
Начнем с определения ОДЗ:
При умножении обеих частей уравнения на единый знаменатель всех дробей и сокращении аналогичных выражений, которые записаны в числителе и знаменателе, получим:
Прибегая к арифметическим преобразованиям, можно записать уравнение в упрощенной форме:
Второе значение не соответствует области допустимых значений.
Общие сведения
Математика — наука о числах и действиях над ними. Значение, которое можно записать в виде обыкновенной дроби, называют рациональным. Оно состоит из целого числа в числителе и натурального в знаменателе. Простое выражение можно представить как бесконечную десятичную дробь. Множество рациональных чисел обозначают латинской буквой Q. Если действительное значение не рациональное, оно иррациональное.
Выражения могут быть представлены в нестандартном виде, поэтому приходится выполнять дополнительные преобразования. Это возможно, так как делимое и делитель являются самодостаточными. Упрощения выполняются путём разложения на множители. При этом по возможности следует выполнять действия как для числителя, так и знаменателя. Операции преобразования включают в себя:
Наиболее часто вызывает сложность подбор общего знаменателя. Это приведение основывается на основном свойстве дроби. Согласно ему, умножение на ненулевой многочлен одновременно делимого и делителя не приводит к изменению результата. Отсюда следует, что числитель и знаменатель можно возводить в квадрат, извлекать корень.
Для успешного выполнения действий важно знать формулы сокращённого умножения. Это базисные знания, без которых решать рациональные дроби в 8 классе будет невозможно.
Всего используется 7 теорем: разность кубов и квадратов, произведение разности и суммы, куб суммы и разности, умножение на неполный квадрат. Используя знания, полученные в седьмом классе, многие операции можно выполнять в уме и приводить многочлен к стандартному виду без предварительного раскрытия скобок.
Свойства дроби
Пусть имеется множество, каждому члену которого поставлено в соответствие число игрек. Про такое положение говорят, что множеству задана числовая функция: y = f (x), где x Є D. Описывается область определением функции и обозначается как D (f (x)). Множество можно представить как отношение двух многочленов. Когда в числителе стоит многочлен энной степени, а в знаменателе эмной, то f (x) называют рациональным отношением или дробью.
Такие выражения обладают рядом свойств. Основное из них выражают формулой: P (x)/Q (x) = P (x) * R (x) / Q (x) * R (x). Справедливо оно лишь для случая, при котором множества Q (x) и R (x) неравны нулю, при этом R (x) является многочленом. Формулировка свойства звучит следующим образом: делимое и делитель можно помножить на одинаковое выражение. Например, им может быть число, одночлен или другой многочлен.
К другим свойствам относят:
Если равенство f/g =y/x справедливо, при этом y/x = n/m, верным будет и выражение: f/g = n/m. Отсюда следует, что рациональную дробь можно превратить в обыкновенную, если её делитель и делимое можно умножить или разделить на одинаковый многочлен. Единственное условие — он должен быть отличным от нуля.
Рациональную дробь можно представить в виде суммы. Выполняют это действие, основываясь на правиле сложения или вычитания выражений с одинаковыми знаменателями. Например, k * m — k / k+1 = 1/k + (k2 * m — k2 — k — 1) / (k2 + k).
Из свойств рациональных отношений следует, что для вычитания их друг из друга нужно привести члены к общему знаменателю и найти разность числителей. Аналогично поступают и для операции сложения, только вычитание в числителе заменяют складыванием. Произведение же находится простым перемножением делимых и делителей. А вот деление выполняют по-другому. Чтобы найти частное, нужно первое выражение умножить на обратную вторую дробь. Чтобы возвести дробь в степень, нужно отдельно в неё возвести числитель и знаменатель. По тому же принципу извлекают и корень.
Понимая, как правильно использовать приведённые свойства, решать задания на контрольной работе в школе будет несложно. Но перед сдачей теста необходимо попрактиковаться в самостоятельном решении.
Изменение знака
Следует отметить, что приём по изменению знака часто используют при разложении рациональных отношений на простейшие дроби. Например, (2×3 — 3) / (- x3 — x). Так как степень числа в числителе меньше чем в знаменателе, нужно использовать разложение. Причём в другом случае пришлось бы применять деление для нахождения целой части. Для удобства действия выражение нужно умножить на минус единицу. В результате несложно будет определить верность равенства: 2×3 + 3 / (x3 + x) = 2 + (-2x + 3) / (x3 + x).
Решение примеров
Самостоятельное решение рациональных дробей в алгебре в 8 классе строится на цепочке преобразований. Первое, что нужно сделать — оценить возможность разложения отношения на множители. Для этого лучше использовать формулы сокращённого умножения или дискриминант. Алгоритм преобразований можно представить в следующем виде:
Вот 3 типовые задачи, которые обычно предлагают решить студентам при сдаче зачёта:
При упрощении рациональных отношений сложность связана с тем, что не всегда просто найти общий множитель для числителя и знаменателя. Причём он и не всегда существует, поэтому и нужно пробовать разложение на множители. Если такого члена нет, дробь упростить нельзя.
Дробные рациональные выражения
Содержание:
Дробные рациональные выражения
Дробные рациональные выражения — это выражения, составленные из чисел и переменных с использованием действий сложения, вычитания, умножения и деления на число, отличное от нуля. Дробные выражения допускают также деление на выражение с переменными. Целые и дробные выражения называют рациональными выражениями.
Рациональная дробь и ее основное свойство
Любое дробное выражение (см. п. 48) можно преобразовать к виду 

Примеры рациональных дробей:
Основное свойство дроби выражается тождеством 


Значит,
Например,
Сокращение рациональных дробей
Сократить дробь — это значит разделить числитель и знаменатель дроби на их общий множитель. Возможность такого сокращения обусловлена основным свойством дроби.
Для того чтобы сократить рациональную дробь, нужно числитель и знаменатель разложить на множители. Если окажется, что числитель и знаменатель имеют общие множители, то дробь можно сократить. Если общих множителей нет, то преобразование дроби посредством сокращения невозможно.
Пример:
Сократить дробь
Решение:
Имеем
Значит,
Сокращение дроби выполнено при условии
Приведение рациональных дробей к общему знаменателю
Общим знаменателем нескольких рациональных дробей называют целое рациональное выражение, которое делится на знаменатель каждой дроби (см. п. 54).
Чтобы несколько рациональных дробей привести к общему знаменателю, нужно:
1) разложить знаменатель каждой дроби на множители;
2) составить общий знаменатель, включив в произведение все множители полученных в п. 1) разложений; если некоторый множитель имеется в нескольких разложениях, то он берется с показателем степени, равным наибольшему из имеющихся;
3) найти дополнительные множители для каждой из дробей (для этого общий знаменатель делят на знаменатель дроби);
4) домножив числитель и знаменатель каждой дроби на соответствующий дополнительный множитель, привести дроби к общему знаменателю.
Пример:
Привести к общему знаменателю дроби
Решение:
Разложим знаменатели дробей на множители:
В общий знаменатель надо включить следующие множители: 
Дополнительные множители: для первой дроби 


Сложение и вычитание рациональных дробей
Сумма двух (и вообще любого конечного числа) рациональных дробей с одинаковыми знаменателями тождественно равна дроби с тем же знаменателем и с числителем, равным сумме числителей складываемых дробей:
Аналогично обстоит дело в случае вычитания дробей с одинаковыми знаменателями:
Пример 1.
Упростить выражение
Решение:
Выполним сложение данных дробей:
Для сложения или вычитания рациональных дробей с разными знаменателями нужно прежде всего привести дроби к общему знаменателю, а затем выполнить операции над полученными дробями с одинаковыми знаменателями.
Пример 2.
Упростить выражение
Решение:
Имеем
Умножение и деление рациональных дробей
Произведение двух (и вообще любого конечного числа) рациональных дробей тождественно равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей перемножаемых дробей:
Частное от деления двух рациональных дробей тождественно равно дроби, числитель которой равен произведению числителя первой дроби на знаменатель второй дроби, а знаменатель — произведению знаменателя первой дроби на числитель второй дроби:
Сформулированные правила умножения и деления распространяются и на случай умножения или деления на многочлен: достаточно записать этот многочлен в виде дроби со знаменателем 1.
Учитывая возможность сокращения рациональной дроби, полученной в результате умножения или деления рациональных дробей, обычно стремятся до выполнения этих операций разложить на множители числители и знаменатели исходных дробей.
Пример 1.
Выполнить умножение
Решение:
Использовав правило умножения дробей, получим
Пример 2.
Выполнить деление
Решение:
Использовав правило деления дробей, получим
Возведение рациональной дроби в целую степень
Чтобы возвести рациональную дробь 

Пример 1.
Преобразовать в дробь степень
Решение:
Применив правила возведения в степень дроби и одночлена, получим
При возведении дроби в целую отрицательную степень используется тождество 
Пример 2.
Преобразовать в дробь выражение
Решение:
Преобразование рациональных выражений
Преобразование любого рационального выражения сводится к сложению, вычитанию, умножению и делению рациональных дробей, а также к возведению дроби в натуральную степень. Всякое рациональное выражение можно преобразовать в дробь, числитель и знаменатель которой — целые выражения; в этом, как правило, состоит цель тождественных преобразований рациональных выражений.
Пример:
Решение:
Выполняя действия с рациональными дробями, получим:
Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:
Смотрите также дополнительные лекции по предмету «Математика»:
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.