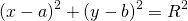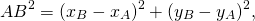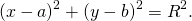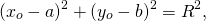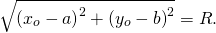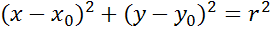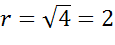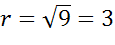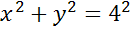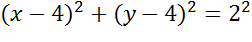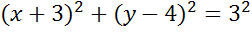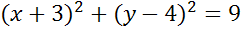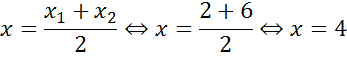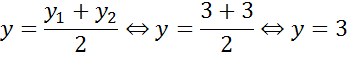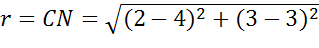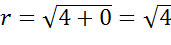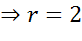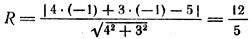Уравнение окружности
Уравнение окружности с центром в точке (a;b) и радиусом R в прямоугольной системе координат имеет вид
1. Пусть в прямоугольной системе координат задана окружность с центром в точке A (a;b) и радиусом R (R>0).

По определению окружности, расстояние от центра до любой точки окружности равно радиусу R, то есть AB=R.
Так как B (x;y) — произвольная точка окружности, координаты любой точки окружности удовлетворяют этому уравнению.
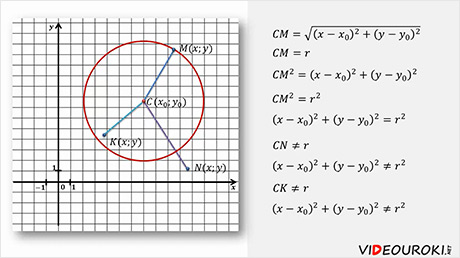
2. Если пара чисел (xo;yo) удовлетворяет данному уравнению, то
А это значит, что расстояние между точками C(xo;yo) и A(a;b) равно R. Значит, точка C(xo;yo) принадлежит окружности с центром в точке A(a;b) и радиусом R.
Следовательно, данное уравнение фигуры является уравнением окружности.
Уравнение окружности.
Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.
В формулировке окружности упоминается расстояние между точкой окружности и центром.
Формула расстояния между двумя точками М1(х1; у1) и М2(х2; у2) имеет вид:
,
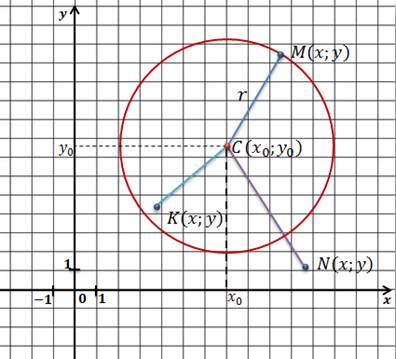
Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х0; у0) и радиусом r.
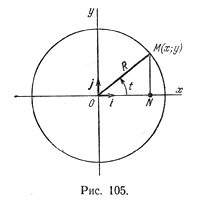
Отметим произвольную точку М(х; у) на этой окружности.
.
Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.
Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х0 ) 2 +(у – у0 ) 2 = r 2 .
Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х0; у0) и радиусом r имеет вид:
В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):
Уравнение окружности
Урок 16. Геометрия 9 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Уравнение окружности»
Прежде всего, давайте вспомним, формулу расстояния между двумя точками и еще, повторим, что уравнение с двумя переменными x и y называется уравнением линии l, если этому уравнению удовлетворяют координаты любой точки линии l и не удовлетворяют координаты никакой точки, не лежащей на этой линии.
Сегодня на уроке мы попробуем по геометрическим свойствам линии найти ее уравнение.
В качестве линии рассмотрим окружность радиуса 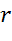
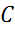
Задача. Записать уравнение окружности с радиусом 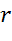
Начало координат имеет координаты (0;0). Подставим их в уравнение окружности и получим, что уравнение окружности с радиусом r и центром в начале координат имеет вид
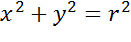
Задача. Начертить окружность, заданную уравнением 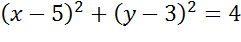
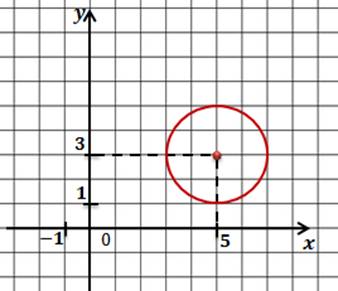
Запишем общее уравнение окружности и проанализируем исходное уравнение. Прежде всего, определимся с координатами центра окружности. Это будут числа 5 и 3. Теперь давайте определим величину радиуса окружности.
Поскольку в правой части формулы стоит квадрат радиуса, то для того, чтобы найти радиус надо извлечь квадратный корень из 4. Получим 2.
Значит наша формула задает окружность с центром в точке с координатами пять три и радиусом равным двум.
Задача. Начертить окружность, заданную уравнением 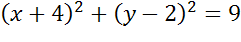
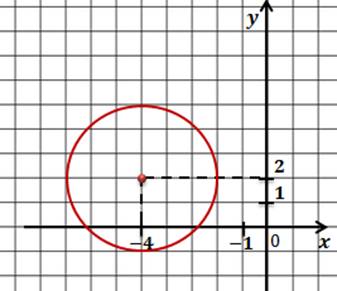
Запишем общее уравнение окружности и проанализируем исходное уравнение. Прежде всего определимся с координатами центра окружности.
Задача. Начертить окружность, заданную уравнением 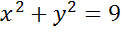
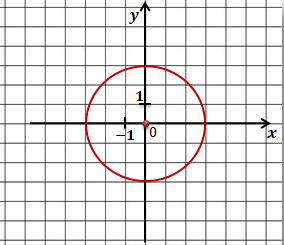
Решение. Уравнениями такого типа описываются окружности с центром в начале координат. Теперь давайте определим величину радиуса окружности. Поскольку в правой части формулы стоит квадрат радиуса, то для того, чтобы найти радиус надо извлечь квадратный корень из 9.
Значит наша формула задает окружность с центром в точке с координатами (0;0) и радиусом равным 3.
Теперь давайте попробуем решить задачу обратную данным.
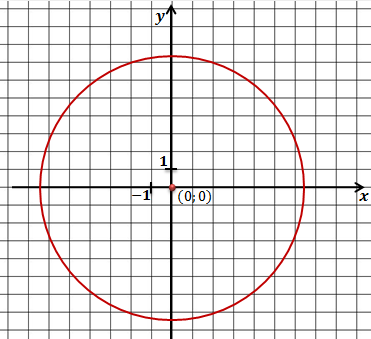
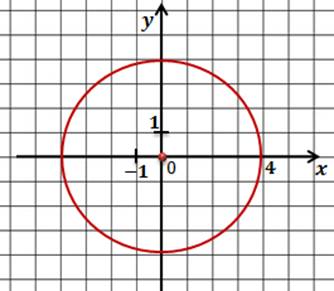
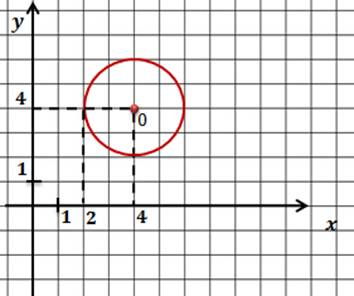
Задача. Составить уравнение окружности, которая показана на рисунке.
Как и в предыдущих задачах мы начнем с определения координат центра окружности. Сделать это нетрудно. Центр этой окружности совпадает с началом координат, поэтому центр окружности имеет координаты (0;0).
Нетрудно заметить, что радиус окружности равен 4.
Запишем уравнение окружности и подставим найденные значения.
Ответ: 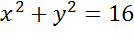
Решим еще одну задачу.
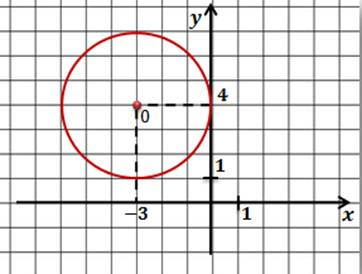
Задача. Составить уравнение окружности, которая показана на рисунке.
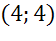
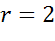
Ответ: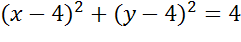
Задача. Составить уравнение окружности, которая показана на рисунке.
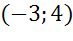
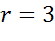
Ответ: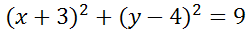
Решая задачи, мы с вами выполняли один и тоже порядок действий. Давайте еще раз повторим этот порядок.
Для того, что бы составить уравнение окружности и построить ее надо:
1. Найти координаты центра окружности.
2. Найти длину радиуса этой окружности.
3. Записать уравнение окружности.
4. Подставить полученные значения в уравнение окружности.
5. Построить окружность, если это требуется для решения задачи.
Рассмотрим еще одну задачу.
Написать уравнение окружности с диаметром эм эн, если точка эн имеет координаты два три, точка эм имеет координаты шесть три.
Задача. Написать уравнение окружности с диаметром 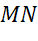
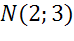
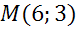
Найдем координаты центра окружности. Центр окружности является серединой диаметра. Воспользуемся формулами для нахождения координат середины отрезка.
Получим, что центр окружности имеет координаты 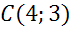
Теперь определим радиус окружности. Для этого найдем расстояние от центра окружности до концов диаметра.
Запишем общее уравнение окружности и подставим в него найденные значения. Тогда получим, что уравнение данной окружности имеет вид:
Ответ: 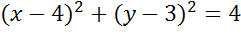
Подведем итоги урока.
На сегодняшнем уроке мы познакомились с формулой, которая задает окружность с центром в точке С (x0; y0) и радиусом r.
Также мы познакомились с формулой, которая задает окружность с центром в начале координат и радиусом r.
Мы рассмотрели задачи на составление уравнения окружности по рисунку и на построение окружности по заданному уравнению.
Уравнение окружности
Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.
Если точка С — центр окружности, R — ее радиус, а М — произвольная точка окружности, то по определению окружности
Равенство (1) есть уравнение окружности радиуса R с центром в точке С.
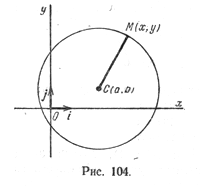
Пусть на плоскости задана прямоугольная декартова система координат (рис. 104) и точка С(а; b) — центр окружности радиуса R. Пусть М(х; у) — произвольная точка этой окружности.
Так как |СМ| = \( \sqrt <(x — a)^2 + (у — b)^2>\), то уравнение (1) можно записать так:
(x — a) 2 + (у — b) 2 = R 2 (2)
Уравнение (2) называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке (а; b). Например, уравнение
есть уравнение окружности радиуса R = 5 с центром в точке (1; —3).
Если центр окружности совпадает с началом координат, то уравнение (2) принимает вид
Уравнение (3) называют каноническим уравнением окружности.
Задача 1. Написать уравнение окружности радиуса R = 7 с центром в начале координат.
Непосредственной подстановкой значения радиуса в уравнение (3) получим
Задача 2. Написать уравнение окружности радиуса R = 9 с центром в точке С(3; —6).
Подставив значение координат точки С и значение радиуса в формулу (2), получим
(х — 3) 2 + (у — (—6)) 2 = 81 или (х — 3) 2 + (у + 6) 2 = 81.
Задача 3. Найти центр и радиус окружности
Сравнивая данное уравнение с общим уравнением окружности (2), видим, что а = —3, b = 5, R = 10. Следовательно, С(—3; 5), R = 10.
Задача 4. Доказать, что уравнение
является уравнением окружности. Найти ее центр и радиус.
Преобразуем левую часть данного уравнения:
Это уравнение представляет собой уравнение окружности с центром в точке (—2; 1); радиус окружности равен 3.
Задача 5. Написать уравнение окружности с центром в точке С(—1; —1), касающейся прямой АВ, если A (2; —1), B(— 1; 3).
Напишем уравнение прямой АВ:
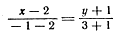
Так как окружность касается данной прямой, то радиус, проведенный в точку касания, перпендикулярен этой прямой. Для отыскания радиуса необходимо найти расстояние от точки С(—1; —1) — центра окружности до прямой 4х + 3y —5 = 0:
Напишем уравнение искомой окружности
Пусть радиус-вектор OM > точки М образует угол величины t с положительным направлением оси Ох, тогда абсцисса и ордината точки М изменяются в зависимости от t
(0 2 = 3 cos 2 t, у 2 = 3 sin 2 t. Складывая эти равенства почленно, получаем
Уравнение с двумя переменными и его график. Уравнение окружности
п.1. Понятие уравнения с двумя переменными
Мы уже знакомы со многими функциями и умеем их записывать в виде формул:
y = 2x + 5 – прямая, y = 5x 2 + 2x – 1 – парабола, \(\mathrm
Если записать такое выражение: x 2 (x + y) = 1 – y – в нём тоже есть две переменные x и y, и постоянная 1.
п.2. Обобщенные правила преобразования графика уравнения
Пусть F(x; y) = 0 – исходный график некоторой функции
Симметричное отображение относительно оси OY
Симметричное отображение относительно оси OX
Центральная симметрия относительно начала координат
Параллельный перенос графика на a единиц вправо
Параллельный перенос графика на a единиц влево
Параллельный перенос графика на b единиц вниз
Параллельный перенос графика на b единиц вверх
Сжатие графика к оси OY в a раз
Сжатие графика к оси OX в b раз
F(x; by) = 0
0 Например:
п.4. Примеры
Пример 1. Постройте график уравнения:
а) 2x + 7y – 14 = 0
Выразим y из уравнения: \( \mathrm
б) xy + 4 = 0
Выразим y из уравнения: \( \mathrm
в) ( x+ 2) 2 + y 2 = 4
Это – уравнение окружности с центром O(–2; 0), радиусом \( \mathrm
г) x 2 + 5y – 2 = 0
Выразим y из уравнения: \( \mathrm
Пример 2*. Постройте график уравнения:
а) 2|x| + 5y = 10
\( \mathrm
Строим график для \( \mathrm
б) 3x + |y| = 6
|y| = –3x + 6
Строим график для y > 0: y = –3x + 6, а затем отражаем его относительно оси OX в нижнюю полуплоскость.
в) |x| + |y| = 2
|y| = –|x| + 2
Строим график для x > 0, y > 0: y = –x + 2, а затем отражаем его относительно осей OX и OY.
г) |x – 1| + |y – 2| = 4
Получим тот же ромб (квадрат), что и в (в), но его центр будет перенесен из начала координат в точку O(1; 2).
д) \(\mathrm<\frac<|x-1|><2>+2|y-2|=4>\)
Ромб по x растянется в 2 раза по диагонали, а по y – сожмётся в 2 раза по диагонали.
Пример 3. Постройте график уравнения:
а) x 2 + y 2 + 4x – 6y + 4 = 0
Выделим полные квадраты:
(x 2 + 4x + 4) + (y 2 – 6y + 9) – 9 = 0
(x + 2) 2 + (y – 3) 2 = 3 2 – уравнение окружности с центром (–2; 3), радиусом 3.