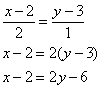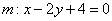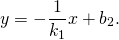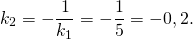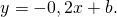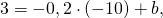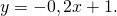Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости онлайн
С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через данную точку и перпендикуляной данной плоскости. Дается подробное решение с пояснениями. Для построения уравнения прямой введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости
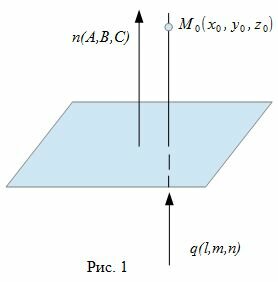
Наша цель построить уравнение прямой, проходящей через данную точку M0 и перпендикулярной к данной плоскости Ax+By+Cz+D=0.
Общее уравнение плоскости имеет вид:
где n(A,B,C)− называется нормальным вектором плоскости.
Уравнение прямой, проходящей через точку M0(x0, y0, z0) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:
 |
Таким образом, уравнение прямой, проходящей через точку M0(x0, y0, z0) и ортогональный плоскости (1) имеет следующий вид:
 |
Общее уравнение плоскости имеет вид (1), где :
Уравнения прямой, которая проходит через заданную точку и перпендикулярна к заданной плоскости.
В этой статье мы разберемся с нахождением уравнений прямой, которая в прямоугольной системе координат в трехмерном пространстве проходит через заданную точку и перпендикулярна к заданной плоскости. Сначала разберем принцип составления уравнений такой прямой, после чего перейдем к решению задач.
Навигация по странице.
Принцип составления уравнений прямой, проходящей через заданную точку перпендикулярно к заданной плоскости.
Прежде чем приступить к составлению уравнений прямой, которая проходит через заданную точку пространства перпендикулярно к заданной плоскости, освежим в памяти один момент.
В 10 классе на уроках геометрии доказывается теорема: через любую точку трехмерного пространства проходит единственная прямая, перпендикулярная к заданной плоскости. Таким образом, мы можем определить конкретную прямую, указав точку, через которую она проходит, и плоскость, к которой она перпендикулярна.
Сформулируем условие задачи.
Итак, задача нахождения уравнений прямой, которая проходит через заданную точку пространства и перпендикулярна к заданной плоскости, решена. Осталось лишь рассмотреть несколько решенных примеров.
Примеры нахождения уравнений прямой, которая проходит через заданную точку пространства и перпендикулярна к заданной плоскости.
В этом пункте статьи мы приведем подробные решения наиболее характерных задач, в которых находятся уравнения прямой, проходящей через заданную точку пространства перпендикулярно к заданной плоскости.
Начнем с самого простого случая, когда требуется написать уравнения прямой, проходящей через заданную точку перпендикулярно к одной из координатных плоскостей.

Аналогично решается задача, в условии которой даны координаты точки, через которую проходит прямая, и задана плоскость с помощью общего уравнения плоскости.

В заключении рассмотрим пример составления уравнений прямой, которая проходит через заданную точку пространства и перпендикулярна к плоскости, заданной тремя не лежащими на одной прямой точками.
Тогда, 

Приведем второй способ решения этой задачи.

Уравнение прямой, проходящей через заданную точку перпендикулярно заданной прямой.
Эта статья о составлении уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой. Сначала даны необходимые теоретические сведения, далее приведены подробные решения характерных примеров, в которых требуется записать уравнение прямой, проходящей через заданную точку перпендикулярно заданной прямой.
Навигация по странице.
Принцип составления уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой.
Прежде чем приступить к нахождению уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой, обговорим некоторые важные моменты.
Таким образом, задача о составлении уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой, имеет практическое значение лишь для случая на плоскости.
Обсудим способы решения этой задачи.
От найденного уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой, можно при необходимости перейти к другому виду уравнения этой прямой.
Решение примеров на составление уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой.
Давайте разберем составление уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой, на примерах.

Составьте уравнение прямой, проходящей через начало прямоугольной декартовой системы координат Oxy перпендикулярно прямой 
Очевидно, 







Напишите уравнение прямой, проходящей через точку 

Угловой коэффициент прямой 






2.5.4. Как найти прямую, перпендикулярную данной?
В отличие от предыдущих задач п. 2.5, рассмотренные ниже схемы работают лишь в декартовой системе координат (но не в общем аффинном случае):
Задача 79
Прямая задана уравнением 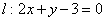
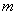
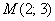
Решение: по условию известна точка 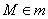
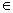
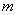
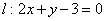
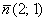
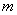
Уравнение прямой 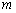
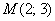
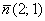
Ответ:
Развернём геометрический этюд: 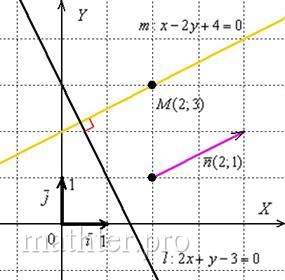
1) Из уравнений 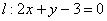
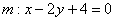
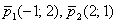
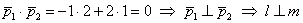
Кстати, можно использовать векторы нормали, это даже проще.
2) Проверяем, удовлетворяет ли точка 
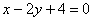
Оба пункта легко выполнить устно!
Задача 80
Найти точку пересечения перпендикулярных прямых 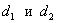
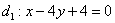
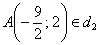
В задаче несколько действий, поэтому решение удобно оформить по пунктам.
И наше увлекательное путешествие продолжается:
Уравнение перпендикулярной прямой
Как составить уравнение прямой перпендикулярной данной прямой и проходящей через данную точку?
Пусть y=k1x+b1 — данная прямая. С учётом условия перпендикулярности прямых уравнение прямой, перпендикулярной данной, имеет вид
Если эта прямая проходит через точку M(xo; yo), то её координаты удовлетворяют уравнению прямой. Подставив в уравнение xo и yo, мы найдем b.
1) Написать уравнение прямой, проходящей через точку A(-10;3), перпендикулярной прямой y=5x-11.
Так как прямые перпендикулярны, если их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку, то
Значит уравнение прямой, перпендикулярной прямой y=5x-11, имеет вид
Так как прямая проходит через точку A(-10;3), то координаты A удовлетворяют уравнению прямой:
Итак, уравнение прямой, перпендикулярной прямой y=5x-11 и проходящей через точку A(-10;3)
Так как искомая прямая проходит через точку M(-5;9), то координаты M удовлетворяют уравнению прямой: y=9.
3) Написать уравнение прямой, перпендикулярной прямой y=4, проходящей через точку F(7;-5).
Прямая y=4 перпендикулярна оси ординат. Следовательно, прямая, уравнение которой мы ищем, параллельна оси ординат, а значит, её уравнение имеет вид x=a.
Так как эта прямая проходит через точку F(7;-5), то координаты F удовлетворяют уравнению прямой: x=7.