Слово Как пишется объем прямоугольного параллелепипеда - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

Объем параллелепипеда

Понятие объема

Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.

Объём — это количественная характеристика пространства, занимаемого телом или веществом.

Другими словами, это то, сколько места занимает предмет.

Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах.

За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см 3 ), кубический миллиметр (1 мм 3 ), кубический метр (1 м 3 ).

Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, сока в графине, земли в клумбе.

Два свойства объёма

Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.

Объем прямоугольного параллелепипеда

Параллелепипед — это многогранник с шестью гранями, каждая из которых является параллелограммом.

Прямоугольным параллелепипедом называют параллелепипед, у которого все грани являются прямоугольниками.

Формула объема прямоугольного параллелепипеда

Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты:

V = a × b × h

Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.

Источник

Как найти объем прямоугольного параллелепипеда?

Прямоугольный параллелепипед, с точки зрения математики, является объемной фигурой с шестью гранями. Увидеть его можно, если посмотреть на прямоугольный бассейн, кирпич или спичечный коробок.

Эта фигура очень часто встречается в повседневной жизни, однако, нередко возникает необходимость узнать ее объем, что для многих представляет некоторые трудности. Например, какого объема необходим бак для воды на дачном участке, или каким размером делать бассейн.

Во многих других ситуациях возникает проблема, как найти объем параллелепипеда правильно.

Между тем вычислить это значение очень просто. Достаточно лишь знать ширину, длину и высоту предмета или объекта. И также необходимо знать формулу, с помощью которой и находят объем данной геометрической фигуры.

Основные особенности и формула для расчета

Для того чтобы найти объем параллелепипеда необходимо:

Это все предельно просто и не таит никаких подводных камней. Главное — это знать требуемые значения, без которых выполнить расчет будет невозможно.

При этом важно знать, что определить параметр можно в сантиметрах, кубометрах, дециметрах и некоторых других размерностях в зависимости от требований. Если говорить о Международной системе единиц (СИ), параметр рассчитывают в сантиметрах. Это оптимальный вариант. Но при желании всегда можно перевести значение в требуемые размерности.

Формула расчета в двух вариантах

Итак, для расчета по формуле нужно знать длину, ширину и высоту измеряемого предмета. Эти данные следует обозначить соответственно как А, B и C, а объем обычно представляют буквой V. Формула для определения объема прямоугольного параллелепипеда при этом будет выглядеть следующим образом: V = A x B x C.

Если определятся объем бассейна, то необходимо его длину, ширину и глубину перемножить. Для более простого восприятия давайте разберем правила расчета объема параллелепипеда на примере. Допустим, что его длина составляет 10 метров, ширина достигает 3 метров, а глубина — 1,5. В этом случае объем этого объекта определяется следующим образом: 10x3x1,5=45 кубометров, или 45 кубических метров.

Можно выделить и другую формулу, которая имеет некоторое отличие. Она представляет собой произведение площади основания на высоту. Формула выглядит следующим образом: V = S x h. Здесь h — высота параллелепипеда. S — площадь основания, которая представлена произведением двух сторон основания. Обычно их обозначают, как a и b: S = a x b.

При расчете можно пользоваться любой из двух приведенных формул. Обе являются верными и позволяют получить точные данные. Последний вариант удобен, когда уже известна площадь основания. Если же она неизвестна, проще перемножать сразу три линейных размера, исключая необходимость в лишней процедуре.

О чем еще следует знать для правильности расчета?

Для вычисления объема параллелепипеда необходимо понять, что это за фигура. Она представляет собой призму, основание которой — параллелограмм. Параллелепипед имеет 6 граней, каждый из которых является параллелограммом. При этом выделяют несколько видов фигур. Принцип расчета не имеет конкретных отличий, но сами фигуры внешне отличаются. Итак, можно выделить такие виды:

И также важно помнить о том, что в процессе выполнения расчета у каждой составляющей формулы должна быть одна и та же размерность. Если опустить это простое правило, получить верный результат не удастся. Если вы выполняете расчеты просто на уроках математики, проблемой могут стать только неудовлетворительные оценки. А при проектировании и наличии ошибок в расчетах проблемы могут быть более серьезными.

Не стоит думать, что основные математические формулы по определению объемов геометрических фигур встречаются исключительно на уроках математики. В большинстве случаев они пригодятся и в последующей жизни. В частности, во время ремонтных или строительных работ, при проектировании и декорированию интерьера, а также в ряде других случаев. Именно тогда без правильной формулы обойтись не удастся.

Можно подвести итог: объем параллелепипеда равен произведению трех линейных размеров — длины, ширины, высоты. Параметр напрямую зависит от трех единиц измерения при любом вращении и повороте. Результат будет неизменным.

Видео

Видео поможет вам научиться находить объем прямоугольного параллелепипеда.

Источник

Объемы фигур. Объем параллелепипеда.

Объем прямоугольного параллелепипеда, формула.

Параллелепипедом является призма, основание у которой – это параллелограмм. У параллелепипеда

6 граней, а они, в свою очередь, являются параллелограммами.

Прямой параллелепипед, у которого все 6 граней прямоугольники, является прямоугольным.

Другими словами, прямоугольный параллелепипед — это объемная фигура, у которой есть 6 граней, и

Объем прямоугольного параллелепипеда равен произведению площади основания на высоту:

a – длина параллелепипеда,

b – ширина параллелепипеда,

Примеры прямоугольного параллелепипеда: спортивный зал, кирпич, картонная коробка или столешница

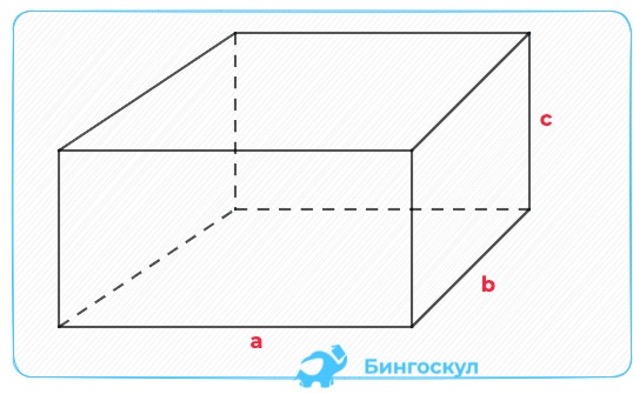
Длины 3 рёбер прямоугольного параллелепипеда, которые имеют общий конец, называются измерениями

прямоугольного параллелепипеда.

Прямоугольный параллелепипед с одинаковыми измерениями является кубом. Все 6 граней куба — это

Квадрат длины диагонали прямоугольного параллелепипеда = сумме квадратов 3 его измерений.

Объем прямого параллелепипеда, формула.

Как найти объем параллелепипеда?

Площадь боковой поверхности параллелепипеда, формула:

где Р_о — периметр основания,

Площадь полной поверхности, формула

где S_о — площадь основания

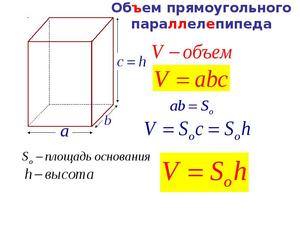
Формула объёма прямого параллелепипеда:

Объем произвольного параллелепипеда.

Объём и соотношения в наклонном параллелепипеде часто определяются с помощью векторной алгебры.

Чему равен объём параллелепипеда? Объем параллелепипеда равен абсолютной величине смешанного

произведения трёх векторов, которые определяются 3-мя сторонами параллелепипеда, которые исходят

Соотношение длина сторон параллелепипеда – угол между ними даёт утверждение, что определитель

Грама указанных 3х векторов равен квадрату их смешанного произведения.

Источник

Формулы вычисления объёма прямоугольника и параллелепипеда

Школа — это необъятная чаша знаний, которая включает в себя множество дисциплин, которые могут заинтересовать любого ребенка. Математика — царица точных наук. Строгая и дисциплинированная, она не терпит неточностей. Даже повзрослев, в обычной жизни мы можем столкнуться с разными математическими проблемами: вычисление квадратных метров для укладки плитки в ванной, кубических метров для определения объема бака и т. д., чего уж говорить о школьниках, которые только-только начинают свой математический путь.

Очень часто, начав изучать математику, точнее, геометрию, ученики путают плоские фигуры с объемными. Куб называют квадратом, шар — кругом, параллелепипед обычным прямоугольником. И здесь есть свои тонкости.

Сложно помочь ребенку в выполнении домашнего задания, не зная точно, объем или площадь какой фигуры — плоской или же объемной, нужно найти. Невозможно найти объем плоских фигур, таких как квадрат, круг, прямоугольник. В их случае можно найти лишь площадь. Прежде чем переходить к выполнению задачи, следует подготовить нужные атрибуты:

Вычисление объема прямоугольного параллелепипеда

Итак, вы знаете, что нужно рассчитать объем, но не забывайте, что обязательно нужно уточнить о какой именно фигуре идет речь: объем куба, или же объемного прямоугольника. Ведь расчет этих, казалось бы, одинаковых фигур, абсолютно разный.

Для начала рассмотрим само понятие объемного прямоугольника. Это параллелепипед. В его основании находится параллелограмм. Так как таковых у него шесть, следовательно все параллелограммы являются гранями параллелепипеда.

Что касается его граней, они могут отличаться, то есть, если прямые боковые грани представляют собой прямоугольники, тогда это прямой параллелепипед, ну, а если все шесть граней являются прямоугольниками, то перед нами прямоугольный параллелепипед.

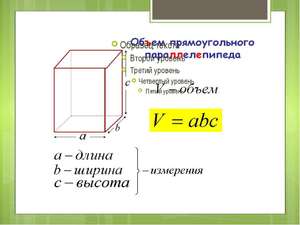
Определив все поставленные задачи, можно переходить непосредственно к вычислениям. Для этого нам понадобятся специальные формулы. Итак, для того чтобы найти объем прямоугольного параллелепипеда перемножается между собой длина, ширина и высота (то есть толщина фигуры). Формула вычисления объема прямоугольного параллелепипеда следующая:

V=a*b*h,

V является объемом параллелепипеда, где a — его длина b — ширина и h — высота соответственно.

Важно! Перед началом перевести все измерения в одну единицу исчисления. Ответ должен получится непременно в кубических единицах.

Пример первый

Определим объем бака для спирта, при следующих размерах:

Для начала обязательно согласовываем единицы измерения и перемножаем их:

Перемножив данные, мы получим ответ в кубических метрах, то есть 3*2.5*3= 22.5 метра в кубе.

Пример второй

Шкаф имеет высоту четыре метра, ширину семьдесят сантиметров и глубину 80 сантиметров.

Зная формулу вычисления можно произвести умножение. Но не стоит торопиться, как и было сказано вначале, следует согласовать между собой единицы, то есть при желании вычислять в сантиметрах перевести все исчисления в сантиметры, ежели в метрах, то в метры. Сделаем оба варианта.

Итак, начнем с сантиметров. Переводим метры в сантиметры:

V = 2240000 сантиметров в кубе.

V = 2.24 метра в кубе.

Исходя из вышеперечисленных манипуляции, очевидно, что работа с кубическими метрами более легка и понятна.

Пример третий

Дана комната, объем которой должен быть вычислен. Длина этой комнаты равна пяти метрам, ширина — трем, а высота потолка 2,5. Опять используем известную нам формулу:

V = a * b * h;

где, а длина комната и равна 5, b- ширина и равна 3 и h высота, которая равна 2.5

Так как все единицы даны в метрах, можно сразу приступать к вычислениям. Перемножая между собой a, b и h:

V = 37.5 метра в кубе.

Итак, в качестве заключения, можно сказать, что зная основные математические правила для вычисления объема или же площади фигур, а также правильно определив фигуры (плоские или же объемные), умея переводить сантиметры в метры и наоборот — можно облегчить изучение геометрии вашему ребенку, что не может не сделать этот процесс более интересным и привлекательным, ведь все накопленные знания в школе, могут быть успешно использованы в самой обычной бытовой жизни в будущем.

Источник

По какой формуле вычисляется объем прямоугольного параллелепипеда?

Содержание:

Параллелепипед – многогранник, состоящий из шести четырехугольных поверхностей с попарно параллельными сторонами. Различают несколько видов параллелепипедов в зависимости от вида четырехугольников, лежащих в их основе. Рассмотрим, какими они бывают, чем отличаются. Научимся находить площадь и объем прямоугольного и наклонного параллелепипедов по известным формулам.

Прямоугольный параллелепипед

Кубоидом или прямоугольным называется шестигранный многогранник с прямоугольниками в основании. Его противоположные поверхности взаимно параллельны, а сходящиеся в одной вершине – перпендикулярны. Ребра, выходящие из одной вершины, называются измерениями.

Свойства геометрического тела:

Рассмотрим формулы объема прямоугольного параллелепипеда и его площади.

Как найти площадь параллелепипеда

Площадью называется численная характеристика плоской фигуры, показывающая, сколько квадратов со стороной, равной единице, поместятся на её поверхности. Вычисляется как сумма площадей шести поверхностей в виде прямоугольников.

где: ab, bc и ac – площади поверхностей.

Так как стороны парные, получившуюся сумму умножают на два.

Для примера, имеем тело с размерами:

a = 3, b = 4 и c = 5 см.

Полная площадь поверхности равна:

S = 2 * (3*4 + 4*5 + 5*3) = 2 * (12 + 20 +15) = 2 * (47) = 94 см.

Объем параллелепипеда

Объемом называется численная характеристика тела, отражающая занимаемое им пространство. Определяется как количество кубов со стороной единица, которое поместится в многоугольнике.

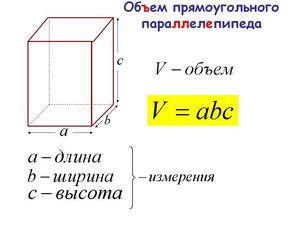
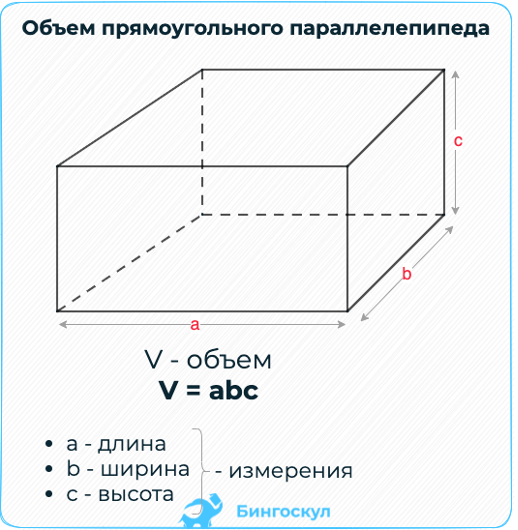
Объем прямоугольного параллелепипеда вычисляется по формуле: V = a * b * c, где

a, b, c – размеры измерений, выходящих из одной точки, или длина, ширина и высота многогранника.

Чтобы найти объем прямоугольного параллелепипеда по приведенной формуле, в нее подставляют размеры граней многоугольника, например:

Измеряется в кубических единицах – сантиметрах, метрах и т.д. либо литрах: 1 литр равен 1 дециметру кубическому.

Физический смысл объема прост:

Вторая формула понадобится, когда в исходных данных есть площадь одной из поверхностей (S_осн) и длина третьей грани (h) или высота.

Смысл вычислений остается прежним – перемножить площадь поверхности на длину третьей стороны тела.

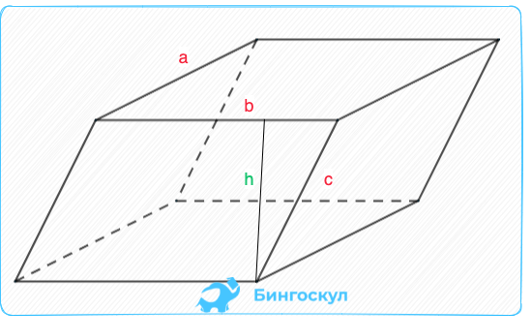
Объем наклонного параллелепипеда

К наклонным параллелепипедам относят четырехугольные призмы с параллелограммом в основании, боковые грани которого относительно него расположены под углом, отличным от 90°.

Площадь и объем наклонного параллелепипеда вычисляются по тем формулам, что и прямоугольного: V = S_осн * h или V = a * b * c.

Площадь определяются иначе, хоть и равна сумме поверхностей боковых граней и оснований.

S = S₁ + S₂ +S_осн. Боковые поверхности – прямоугольники, их площади S₁ b S₂ равны производным ширины на длину прямоугольников, которыми они представлены: a*c и a*b. Размеры оснований – параллелограммов – вычисляются так: S_осн = b * h.

Мы рассмотрели способы, как найти объем основных параллелепипедов по разным формулам в зависимости от исходных данных. В сложных задачах придется применять иные геометрические и тригонометрические формулы для определения требуемых данных.

Источник