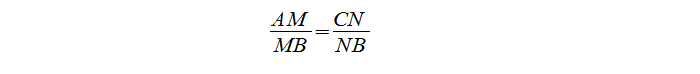Знак подобия в геометрии — правило и примеры обозначения
В учебниках по геометрии часто встречаются задачи на подобие фигур. Какой знак используется для обозначения подобия фигур? Какие фигуры называются подобными? Поговорим обо всем этом в нашей статье.
Определение и знак подобия в геометрии
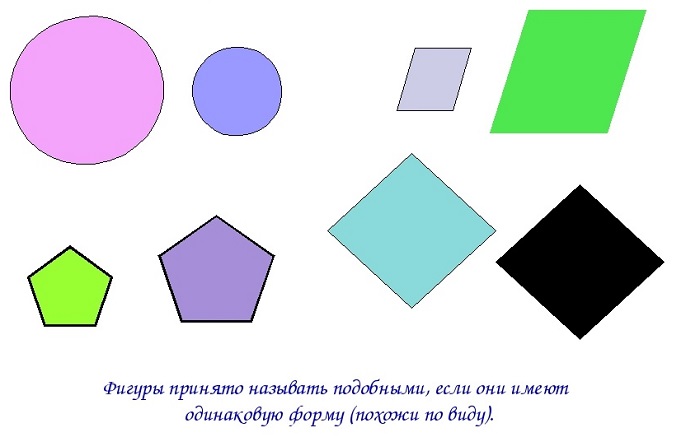
Подобными называются фигуры, если одна из них представляет уменьшенную копию другой.
На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.
Для обозначения термина «подобие» в геометрии используют знак «тильда», который является типографским символом и обозначается волнистой чертой:
∆A 1 B 1 C 1
— треугольники ABC и A1B1C1
подобны.
Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо:
1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.
Коэффициент подобия треугольников и знак подобия
Часто сверху знака подобия выставляют коэффициент подобия треугольников:
В математических задачах и уравнениях «тильду» используют для маркирования разных типов подобия. Часто применяется для обозначения подобия, эквивалентности.
В алгебре высказываний знаком
обозначают логическую операцию «эквиваленция».
При сочетании тильды и знака равенства получают обозначение отношения конгруэнтности, определения в геометрии, применяемого в контексте обозначения равенства различных фигур и тел (углов, отрезков):
Признаки подобия прямоугольных треугольников
Острые углы: наличие равного острого угла в прямоугольных треугольниках делает их подобными.
Два катета: общая пропорциональность катетам одного прямоугольного треугольника к катетам второго делает их подобными.
Катет и гипотенуза: пропорциональность катета и гипотенузы одного прямоугольного треугольника к катету и гипотенузе второго прямоугольного треугольника делает их подобными.
треугольник ∆ABC и треугольник ∆A1B1C1 считаются подобными при равнозначности углов и пропорциональности сторон;
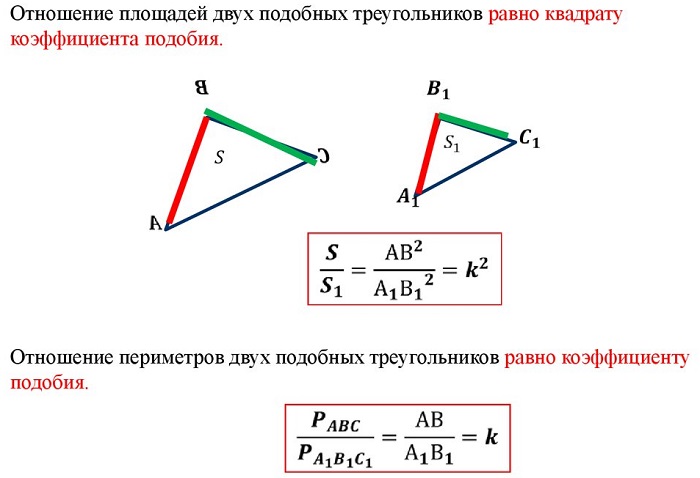
отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство подобия треугольников через среднюю линию
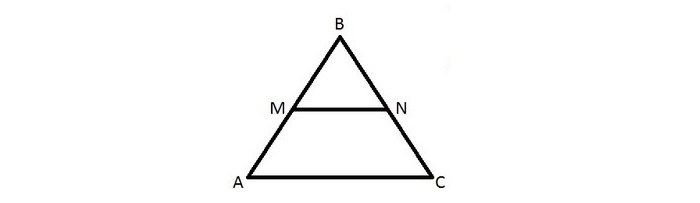
Имеется треугольник ∆ABC, mn — средняя линия. M лежит на AB, N лежит на BC.
Требуется доказательство подобия треугольников ∆MBN и ∆ABC.
Посмотрев на ∆MBN и ∆ABC, видим, что угол В — общий, а отношение:
Отсюда делаем вывод, что ∆MBN
∆ABC по II признаку подобия треугольников, что и требовалось доказать.
Примеры решения задач по геометрии на тему «Подобие треугольников»
Знак подобия в геометрии — правило и примеры обозначения
Определение и знак подобия в геометрии
Подобными называются фигуры, если одна из них представляет уменьшенную копию другой.
На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.

Для обозначения термина «подобие» в геометрии используют знак «тильда», который является типографским символом и обозначается волнистой чертой:

∆A 1 B 1 C 1
— треугольники ABC и A1B1C1
подобны.
Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо:
1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.
Коэффициент подобия треугольников и знак подобия
Часто сверху знака подобия выставляют коэффициент подобия треугольников:

В математических задачах и уравнениях «тильду» используют для маркирования разных типов подобия. Часто применяется для обозначения подобия, эквивалентности.
В алгебре высказываний знаком
обозначают логическую операцию «эквиваленция».
При сочетании тильды и знака равенства получают обозначение отношения конгруэнтности, определения в геометрии, применяемого в контексте обозначения равенства различных фигур и тел (углов, отрезков):

Признаки подобия прямоугольных треугольников
Острые углы: наличие равного острого угла в прямоугольных треугольниках делает их подобными.
Два катета: общая пропорциональность катетам одного прямоугольного треугольника к катетам второго делает их подобными.
Катет и гипотенуза: пропорциональность катета и гипотенузы одного прямоугольного треугольника к катету и гипотенузе второго прямоугольного треугольника делает их подобными.

треугольник ∆ABC и треугольник ∆A1B1C1 считаются подобными при равнозначности углов и пропорциональности сторон;
отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство подобия треугольников через среднюю линию
Имеется треугольник ∆ABC, mn — средняя линия. M лежит на AB, N лежит на BC.

Требуется доказательство подобия треугольников ∆MBN и ∆ABC.
Посмотрев на ∆MBN и ∆ABC, видим, что угол В — общий, а отношение:

Отсюда делаем вывод, что ∆MBN
∆ABC по II признаку подобия треугольников, что и требовалось доказать.
Примеры решения задач по геометрии на тему «Подобие треугольников»



В учебниках по геометрии часто встречаются задачи на подобие фигур. Какой знак используется для обозначения подобия фигур? Какие фигуры называются подобными? Поговорим обо всем этом в нашей статье.
Определение и знак подобия в геометрии
На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.
Для обозначения термина «подобие» в геометрии используют знак «тильда», который является типографским символом и обозначается волнистой чертой:
Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо:
1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.
Коэффициент подобия треугольников и знак подобия
Часто сверху знака подобия выставляют коэффициент подобия треугольников:
В математических задачах и уравнениях «тильду» используют для маркирования разных типов подобия. Часто применяется для обозначения подобия, эквивалентности.
В алгебре высказываний знаком
обозначают логическую операцию «эквиваленция».
При сочетании тильды и знака равенства получают обозначение отношения конгруэнтности, определения в геометрии, применяемого в контексте обозначения равенства различных фигур и тел (углов, отрезков):
Признаки подобия прямоугольных треугольников
Острые углы: наличие равного острого угла в прямоугольных треугольниках делает их подобными.
Два катета: общая пропорциональность катетам одного прямоугольного треугольника к катетам второго делает их подобными.
Катет и гипотенуза: пропорциональность катета и гипотенузы одного прямоугольного треугольника к катету и гипотенузе второго прямоугольного треугольника делает их подобными.
треугольник ∆ABC и треугольник ∆A1B1C1 считаются подобными при равнозначности углов и пропорциональности сторон;
отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство подобия треугольников через среднюю линию
Требуется доказательство подобия треугольников ∆MBN и ∆ABC.
Посмотрев на ∆MBN и ∆ABC, видим, что угол В — общий, а отношение:
Отсюда делаем вывод, что ∆MBN
∆ABC по II признаку подобия треугольников, что и требовалось доказать.
Примеры решения задач по геометрии на тему «Подобие треугольников»
Знак в геометрии подобен – Знак подобия в геометрии
Знак подобия в геометрии
Определение и знак подобия в геометрии
Обозначают подобие треугольников знаком «».
Пример. (читают: треугольник подобен треугольнику ).
Коэффициент подобия треугольников и знак подобия
Знак «» представляет собой типографский знак «тильда», который изображается в виде волнистой черты. Этот знак может быть как надстрочным, так и междустрочным.
В математике «тильда» используется для обозначения различных видов отношений эквивалентности, в частности, отношения подобия.
Знак «тильда» (или «двойная тильда» ), который стоит перед числом может означать «примерно», «приблизительно равно».
В алгебре высказываний знак «» обозначает логическую операцию «эквиваленция».
Если знак «тильда» сочетать со знаком равенства: «», то он будет обозначать отношение конгруэнтности.
Также знак «тильда» активно используется в информатике и вычислительной технике. Например, в редакторе Tex этот знак означает «неразрывный пробел».
Знак подобия треугольников в геометрии — что значит «
» в геометрии? — 22 ответа
В разделе Школы на вопрос что значит «
» в геометрии? заданный автором Нету лучший ответ это Это знак «Приблизительно»
Ответ от 22 ответа[гуру]
Привет! Вот подборка тем с ответами на Ваш вопрос: что значит «
Ответ от Mitternacht[гуру]
Вроде приблизительно
Ответ от Невропатолог
Ответ от Недоносок[новичек]
Это значит приблизительно
Ответ от МiRaMih[гуру]
Подобие
Ответ от Антон Рзаханов[активный]
это знак подобия)) мы щас проходим)
Ответ от Hip-hop4live[гуру]
Подобие.
Ответ от Ёаша Рощин[активный]
Прекрасных комедий множество. Но одна из лучших «Не упускай из виду! » 1975г. с Пьером Ришаром.
Узнал об этом фильме у него на спектакле в Москве феврале в этом году. Решил посмотреть этот фильм, у меня была истерика, чуть упал под стол от смеха, особенно когда он бегал с унитазом на ноге )) А на самом спектакле Ришар такие байки травил, особенно про Депардье, что я реально устал смеяться )
Ответ от Влад Матвеев[новичек]
подобие
Ответ от Supreme[новичек]
Подобие )
Признаки подобия треугольников на Википедии
Посмотрите статью на википедии про Признаки подобия треугольников
Ответить на вопрос:
что значит «
точно не уверенна, но может подобие Для тех кто пишет приблизительно: знак приблизительности похож на знак =,только линии там волнистые, как в вопросе
Это значит приблизительно
это знак подобия)) мы щас проходим)
Это «тильда», она обозначает «подобие» в геометрии.
Что в Геометрий обозначает недорисованная, перевёрнутая 8-ка?
лежащая на боку 8 знак бесконечности …
Перевёрнутая восьмёрка выглядит также как обычная. Интеграл, параграф. Больше не знаю. У меня была тройка по геометрии (((
в геометрии такой знак обозначает подобие фигур
Я насколько помню так всю жизнь обозначали подобие, НО такого символа фактически нет. Это
и она не настолько загнута по краям, как её в школах рисовали.
Перевернутая восьмерка обозначает бесконечность
Как называется этот знак (Геометрия).
Дуга выгнута вверх? Тогда это знак пересечения. Если выгнута вниз — объединение…. Если я, конечно, вспомнила правильно
он так и называется дуга. а читается например дуга ОВ
Вероятно ето пересечение, если на U похоже.
Это значит точка О получается пересечением АВ и СД. Может это знак пересечения? Больше на ум ничего не идет, что смысл бы имело…
Если дуга выгнута вниз, значит это «дуга», а если вверх то «пересечение».
Знак подобия в геометрии
Подобные треугольники
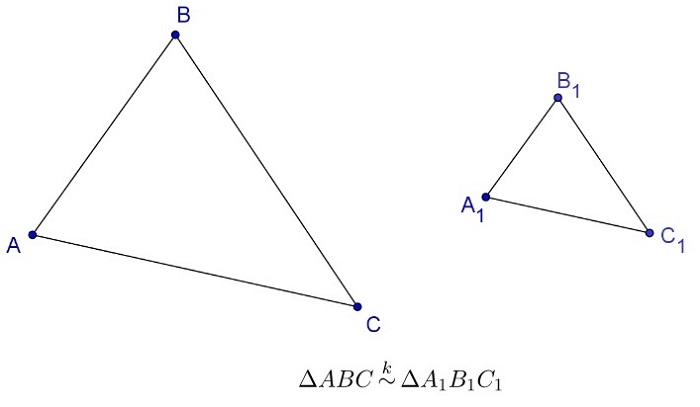
Подобные треугольники — треугольники, у которых соответствующие углы равны, а стороны пропорциональны сходственным сторонам. То есть △ABC∼△A1B1C1\bigtriangleup ABC\sim \bigtriangleup A_1B_1C_1△ABC∼△A1B1C1 означает, что ∠A=∠A1\angle A=\angle A_1∠A=∠A1, ∠B=∠B1\angle B=\angle B_1∠B=∠B1, ∠C=∠C1\angle C=\angle C_1∠C=∠C1, ABA1B1=BCB1C1=ACA1C1\frac
Для того чтобы треугольники △ABC\bigtriangleup ABC△ABC и △A1B1C1\bigtriangleup A_1B_1C_1△A1B1C1 были подобны, достаточно, чтобы выполнялось одно из условий:
1. У △ABC\bigtriangleup ABC△ABC и △A1B1C1\bigtriangleup A_1B_1C_1△A1B1C1 есть две пары равных углов, например ∠A=∠A1\angle A=\angle A_1∠A=∠A1 и ∠B=∠B1\angle B=\angle B_1∠B=∠B1;
2. У △ABC\bigtriangleup ABC△ABC и △A1B1C1\bigtriangleup A_1B_1C_1△A1B1C1 есть пара равных углов, примыкающие к ним стороны пропорциональны, например ∠A=∠A1\angle A=\angle A_1∠A=∠A1 и ABA1B1=ACA1C1\frac
3. У △ABC\bigtriangleup ABC△ABC и △A1B1C1\bigtriangleup A_1B_1C_1△A1B1C1 стороны пропорциональны: ABA1B1=ACA1C1=BCB1C1\frac
Почему символы не отображаются?
Да, бывает и такое, что вместо желанного символа в Ворде или браузере отображаются пустые квадратики. У меня такое было, кости маджонга не отобразились в Либре, а египетские иероглифы даже Хром не стал показывать. Некоторые фазы луны не показывает Хром, и текстовой редактор, а вот в Мозилле все отлично. Так в чем же дело?
На самом деле причина несколько:
У Хрома есть такая болезнь, не каждая сборка поддерживает те или иные символы.
Но, я вас уверяю, символ должен быть, действительно, не самым, что называется, ходовым. А все базовые значки есть практически везде.
Примеры подобных треугольников
Подобны следующие виды треугольников:
Свойства параллельности (антипараллельности) сторон родственных треугольников
Обобщения
Аналогично определяется подобие (с сохранением указанных выше свойств) в 3-мерном евклидовом пространстве, а также в n-мерном евклидовом и псевдоевклидовом пространствах.
В метрических пространствах так же, как в n<\displaystyle n>-мерных римановых, псевдоримановых и финслеровых пространствах подобие определяется как преобразование, переводящее метрику пространства в себя с точностью до постоянного множителя.
Совокупность всех подобий n-мерного евклидова, псевдоевклидова, риманова, псевдориманова или финслерова пространства составляет r<\displaystyle r>-членную группу преобразований Ли, называемой группой подобных (гомотетических) преобразований соответствующего пространства. В каждом из пространств указанных типов r<\displaystyle r>-членная группа подобных преобразований Ли содержит (r−1)<\displaystyle (r-1)>-членную нормальную подгруппу движений.
Примеры подобных треугольников
Подобны следующие виды треугольников:
Свойства параллельности (антипараллельности) сторон родственных треугольников
Типы тетраэдров.
Правильный тетраэдр — это такая правильная треугольная пирамида, каждая из граней которой оказывается равносторонним треугольником.
У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину.
Тетраэдр состоит из 4 граней, 4 вершин и 6 ребер.
Правильный тетраэдр — это один из 5-ти правильных многогранников.
Кроме правильного тетраэдра, заслуживают внимания такие типы тетраэдров:
— Равногранный тетраэдр, у него каждая грань представляет собой треугольник. Все грани-треугольники такого тетраэдра равны.
— Ортоцентрический тетраэдр, у него каждая высота, опущенная из вершин на противоположную грань, пересекается с остальными в одной точке.
— Прямоугольный тетраэдр, у него каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине.
— Каркасный тетраэдр — тетраэдр, который таким условиям:
— Соразмерный тетраэдр, бивысоты у него одинаковы.
— Инцентрический тетраэдр, у него отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке.
Символы в Unicode
Астрономические символы в Unicode
Друзья, в этой статье, только те символы, которые работают в моей системе. Есть несколько не отобразившихся у меня в хроме и документе фаз луны, но я, все равно, их добавила.
Разные астрономические символы
Генетическая символика:
Генетическая символика широко используется для записи результатов скрещивания (гибридизации), решения теоретических и практических задач
Например, при покупке семян сельскохозяйственных культур для посева, надо обращать внимание на значок F1. Он означает, что это гибрид первого поколения, полученный при скрещивании родительских форм
Этот потомок будет обладать ценными характеристиками, ради которых его получали (высокой урожайностью, транспортабельностью и др.). Однако, при посеве семян, собранных с гибридов первого поколения, можно уже не получить растения с нужными свойствами.
Свойства
Формулы площади треугольника
Формула площади треугольника по стороне и высотеПлощадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
Формула площади треугольника по трем сторонам
где = + + 2 — полупериметр треугльника.
Формула площади треугольника по двум сторонам и углу между ними Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
Формула площади треугольника по трем сторонам и радиусу вписанной окружностиПлощадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
Обобщения
Аналогично определяется подобие (с сохранением указанных выше свойств) в 3-мерном евклидовом пространстве, а также в n-мерном евклидовом и псевдоевклидовом пространствах.
В метрических пространствах так же, как в n<\displaystyle n>-мерных римановых, псевдоримановых и финслеровых пространствах подобие определяется как преобразование, переводящее метрику пространства в себя с точностью до постоянного множителя.
Совокупность всех подобий n-мерного евклидова, псевдоевклидова, риманова, псевдориманова или финслерова пространства составляет r<\displaystyle r>-членную группу преобразований Ли, называемой группой подобных (гомотетических) преобразований соответствующего пространства. В каждом из пространств указанных типов r<\displaystyle r>-членная группа подобных преобразований Ли содержит (r−1)<\displaystyle (r-1)>-членную нормальную подгруппу движений.
Определение
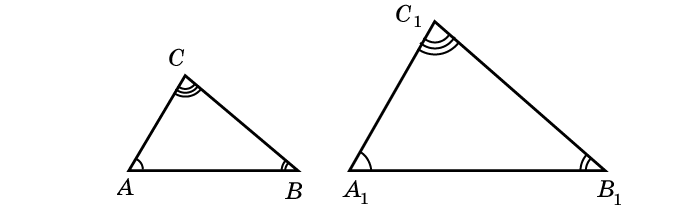
Как правило, два треугольника считаются подобными если они имеют одинаковую форму, даже если они различаются размерами, повернуты или даже перевернуты.
Два треугольника являются подобными если:
1. Каждый угол одного треугольника равен соответствующему углу другого треугольника:∠A1 = ∠A2, ∠B1 = ∠B2 и∠C1 = ∠C2
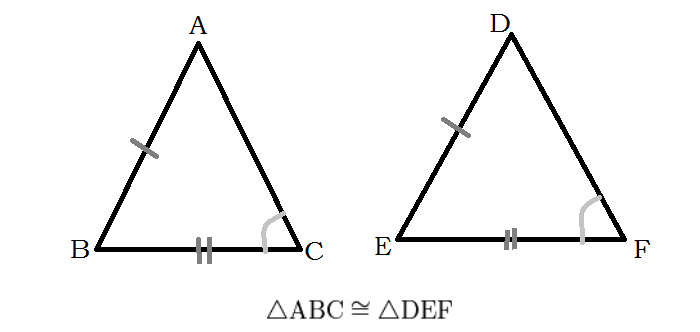
Не нужно путать подобные треугольники с равными треугольниками. У равных треугольников равны соответствующие длины сторон. Поэтому для равных треугольников:
Из этого следует что все равные треугольники являются подобными. Однако не все подобные треугольники являются равными.
Несмотря на то, что вышеприведенная запись показывает, что для выяснения, являются ли два треугольника подобными или нет, нам должны быть известны величины трех углов или длины трех сторон каждого треугольника, для решения задач с подобными треугольниками достаточно знать любые три величины из указанных выше для каждого треугольника. Эти величины могут составлять различные комбинации:
1) три угла каждого треугольника (длины сторон треугольников знать не нужно).Или хотя бы 2 угла одного треугольника должны быть равны 2-м углам другого треугольника. Так как если 2 угла равны, то третий угол также будет равным.(Величина третьего угла составляет 180 — угол1 — угол2)
2) длины сторон каждого треугольника (углы знать не нужно);
3) длины двух сторон и угол между ними.
Далее мы рассмотрим решение некоторых задач с подобными треугольниками. Сначала мы рассмотрим задачи, которые можно решить непосредственным использованием вышеуказанных правил, а затем обсудим некоторые практические задачи, которые решаются по методу подобных треугольников.
Как вставить символы в Ворде?
Чтобы вставить спецсимволы, например, знаки планет и зодиака при печати в Ворде можно воспользоваться двумя способами: через стандартную вкладку «Вставить», или используя Юникод (Unicode) и клавиатуру.
В первом случае нужно:
выбираете на верхней панели «Вставить» => «Символ»,
выбираете шрифт Аrial Unicode MS и листаете вниз, там и будут знаки всех планет, зодиака, математические операторы и многое другое.
Можно не выбирать какой-то конкретный шрифт, а посмотреть, все, что предлагает система, если ищите что-то эдакое. Но в любом случае, стоит помнить, что Аrial Unicode несколько устарел и там находятся только базовые символы. Чего-то интересненького там немного.
Если по какой-то причине вам этот способ не подошел, то выбираем второй вариант:
переводим раскладку в латиницу (то есть на en);
вводим код в Unicode;
зажимаем клавишу ALT и X (далее сочетание клавиш буду обозначать с плюсом, например ALT+X);
все, наслаждаемся нашим значком.
Есть способ с использованием клавиши NumLock (а вы думали, что она просто так на клавиатуре? =)):
включаем кнопку NumLock (в правой (цифровой) части клавиатуры);
зажимаем ALT и одновременно с зажатой клавишей ALT набираем на цифровом блоке нужную комбинацию, например, для знака нужно набрать ALT+0169;
отжимаем ALT и любуемся значком.
Есть еще один вариант, самый простой:
гуглим нужный символ;
копируем его, затем вставляем в документ;
выделяем и отменяем форматирование текста;
Видите, нет ничего сложно. А самое прекрасное, что никаких дополнительных шрифтов (для обычных символов, которых нет на клавиатуре) загружать в систему не надо. Так как они уже там есть.
Подобные фигуры
Подобные фигуры — фигуры, у которых можно сопоставить точки таким образом, что для любой пары точек AAA и BBB первой фигуры и соответствующих им точек A1A_1A1 и B1B_1B1 второй фигуры выполняется соотношение AB=k⋅A1B1AB=k\cdot A_1B_1AB=k⋅A1B1, где kkk — некоторая постоянная величина. Величина kkk называется коэффициентом подобия.
Свойства подобных фигур
Примеры:1. Все правильные шестиугольники подобны друг другу;2. Квадрат и ромб не подобны друг другу, хотя у любого квадрата и ромба стороны пропорциональны;3. Прямоугольник и квадрат НЕ подобны друг другу, хотя у них все углы равны 90º.
Где найти символы в Ворде, пошаговая инструкция
Символы в документе Word находятся быстро. Откройте на компьютере текстовый редактор Ворда. Далее, нажмите по разделу «Вставка», из меню программы выберите – «Символы» и выбираете варианты символов (Скрин 1).
Затем нажимаете кнопку «Другие символы», чтобы выбрать дополнительные символы для текста. Где найти символы в Ворде? Кликните компьютерной мышью на раздел «Набор», в разделе другие символы (Скрин 2).
Далее, выбираете категории символов:
После того, как нашли символ в списке символов, перейдем к его установке в текст.
В Worde есть возможность устанавливать не только простые символы и специальные формулы. Данную функцию можно найти рядом с функцией «Символ». О том, как писать формулы в Word, рассказывается в статье на блоге: (https://biz-iskun.ru/kak-pisat-formuly-v-vord.html).
Определения и понятия в генетике
Генетика (от греч. «генезис» — происхождение) — наука о закономерностях наследственности и изменчивости живых организмов.
Генетика, как одна из отраслей научного знания, оперирует множеством терминов. Рассмотрим основные: