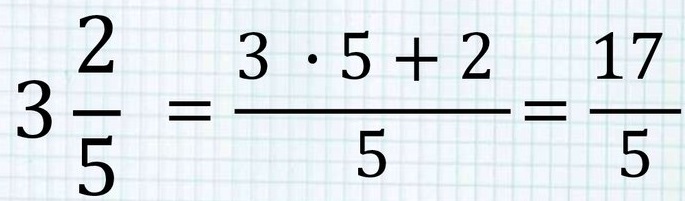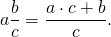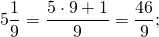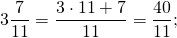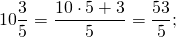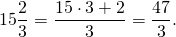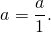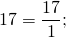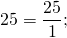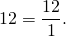Смешанное число можно превратить в неправильную дробь. Это умение необходимо в математических вычислениях. Для этого целую часть нужно умножить на знаменатель и к произведению прибавить числитель нашей дроби. Полученная сумма — это числителем дроби, а знаменателем остается тот же.
3 2/5 – это целое число 3 умножим на знаменатель 5 и прибавим числитель, который был в смешанной дроби (все это пишем над дробной чертой). Это будет числителем, а знаменатель такой же, как в смешанном числе – это 5. Считаем числитель: 3умножить на 5 – это 15 и плюс 2 = 17. Знаменатель – 5. Получилась дробь – 17/5.
1 целая 4/10. Над дробной чертой пишем: 1 умножить на 10 и плюс 4 – это числитель, а знаменатель, как в смешанном числе – 10. Считаем числитель: 1 умножить на 10 = 10 и плюс 4 = 14. Получилась дробь – 14/10.
2 целых 5/8. Над дробной чертой пишем: 2 умножить на 8 и плюс 5 – это числитель, а знаменатель, как в смешанном числе – 8. Считаем числитель: 2 умножить на 8 = 16 и плюс 5 = 21. Получилась дробь – 21/8.
10 целых 2/9. Над дробной чертой пишем: 10 умножить на 9 и плюс 2 – это числитель, а знаменатель, как в смешанном числе – 9. Считаем числитель: 10 умножить на 9 = 90 и плюс 2 = 92. Получилась дробь – 92/9.
20 целых 3/8. Над дробной чертой пишем: 20 умножить на 8 и плюс 3 – это числитель, а знаменатель, как в смешанном числе – 8. Считаем числитель: 20 умножить на 8 = 160 и плюс 3 = 163. Получилась дробь – 163/8.
6 целых 2/5. Над дробной чертой пишем: 6 умножить на 5 и плюс 2 – это числитель, а знаменатель, как в смешанном числе – 8. Считаем числитель: 6 умножить на 5 = 30 и плюс 2 = 32. Получилась дробь – 32/5.
35 целых 4/9. Над дробной чертой пишем: 35 умножить на 9 и плюс 4 – это числитель, а знаменатель, как в смешанном числе – 9. Считаем числитель: 35 умножить на 9 = 315 и плюс 4 = 319. Получилась дробь – 319/9.
61 целая 2/4. Над дробной чертой пишем: 61 умножить на 4 и плюс 2 – это числитель, а знаменатель, как в смешанном числе – 4. Считаем числитель: 61 умножить на 4 = 244 и плюс 2 = 246. Получилась дробь – 246/4.
11 целых 5/8. Над дробной чертой пишем: 11 умножить на 8 и плюс 5 – это числитель, а знаменатель, как в смешанном числе – 8. Считаем числитель: 11 умножить на 8 = 88 и плюс 5 = 93. Получилась дробь – 91/8. 5 целых 6/9. Над дробной чертой пишем: 5 умножить на 9 и плюс 6 – это числитель, а знаменатель, как в смешанном числе – 9. Считаем числитель: 5 умножить на 5 = 45 и плюс 6 = 51. Получилась дробь – 51/9.
Как перевести смешанную дробь в неправильную и наоборот
Объяснения с примерами

Как перевести смешанную дробь в неправильную
Смешанная дробь — это запись целого числа с обыкновенной дробью.
Читается 5 целых три восьмых.
Чтобы нагляднее себе представить, можно мысленно добавлять знак «+» между целым числом и обыкновенной дробью. И это не будет ошибкой, так как знак «плюс» для упрощения записи опускается.
Эта запись означает 5 целых пирогов и 3 восьмых пирога.
5 площадей определенных размеров и 3 восьмых данной площади.

Неправильная дробь — эта та, у которой числитель больше знаменателя. Соответственно, из неё можно выделить 1 целое число или больше. Так как любая неправильная дробь больше единицы.
Можно сделать действие и наоборот — превратить смешанное число в неправильную дробь.
Чтобы перевести смешанное число в неправильную дробь нужно целое число умножить на знаменатель и прибавить числитель. Полученное значение записываем в числитель. Знаменатель оставляем без изменений.
Объяснение почему именно так мы переводим:
Целое число мы можем записать дробью, как сорок восьмых (40: 8 = 5). Не забывайте, что дробь — это деление. Число 40 мы получаем умножением целого числа на знаменатель. Теперь нам осталось сложить две дроби с одинаковыми знаменателями.
Примеры для перевода смешанных дробей в неправильные
Как перевести неправильную дробь в смешанную
Как мы уже говорили, неправильная дробь всегда больше единицы.
Чтобы перевести неправильную дробь в смешанную нужно начать делить числитель на знаменатель до целых. Полученное целое число пишем перед дробью, остаток деления — в числитель. Знаменатель остаётся без изменения.
Схема для запоминания:
Примеры
Как перевести неправильную дробь в правильную
Смешанную дробь иногда называют правильной, поэтому объяснение перевода будет являться дублированием предыдущего абзаца. Если у вас остались вопросы, то смотрите разбор в видео:
Смешанные числа, перевод смешанного числа в неправильную дробь и обратно
В этом материале мы разберем такое понятие, как смешанные числа. Начнем, как всегда, с определения и небольших примеров, потом поясним связь смешанных чисел и неправильных дробей. После этого мы изучим, как правильно выделять целую часть из дроби и получать в результате целое число.
Понятие смешанного числа
Числа вида 0 3 14 также не относятся к смешанным. Здесь не выполняется первая часть условия: целая часть должна быть представлена только натуральным числом, а нуль им не является.
Как соотносятся между собой неправильные дроби и смешанные числа
Эту связь проще всего проследить на конкретном примере.
Наш пример доказывает, что в виде смешанного числа можно представить любую неправильную дробь.
Мы поняли, как приводить неправильную дробь к виду смешанного числа. Если в числителе неправильной дроби стоит такое число, которое можно разделить на знаменатель без остатка, то можно сделать это, и тогда наша неправильная дробь станет натуральным числом.
Как перевести смешанное число в неправильную дробь
Чтобы успешно решать задачи, полезно уметь производить и обратное действие, то есть делать из смешанных чисел неправильные дроби. В этом пункте мы разберем, как правильно это сделать.
Для этого нужно воспроизвести следующую последовательность действий:
1. Для начала представляем имеющееся смешанное число n a b как сумму целой и дробной части. Получается n + a b
2. Далее заменяем целую часть на дробь со знаменателем, равным единице (то есть записываем n как n 1 ).
Разберем это действие на конкретном примере.
Представьте 5 3 7 в виде неправильной дроби.
Решение
Последний шаг – сложение дробей, имеющих разные знаменатели:
5 1 + 3 7 = 35 7 + 3 7 = 38 7
Представьте 15 2 5 в виде неправильной дроби.
Решение
Как выделить из неправильной дроби целую часть
Обычно мы не указываем неправильную дробь в качестве итогового ответа. Принято доводить вычисления до конца и заменять ее либо натуральным числом (разделив числитель на знаменатель), либо смешанным числом. Как правило, первый способ используется, когда разделить числитель на знаменатель можно без остатка, а второй – если такое действие невозможно.
Когда мы выделяем из неправильной дроби целую часть, мы просто заменяем ее равным смешанным числом.
Разберем, как именно это делается.
Приведем доказательство этого утверждения.
Выделение целой части из неправильной дроби a b осуществляется таким образом:
1) производим деление a на b с остатком и записываем неполное частное q и остаток r отдельно.
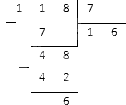
Представьте 107 4 в виде смешанного числа.
Решение
Делим 104 на 7 столбиком:
Нам осталось посмотреть, как заменить неправильную дробь натуральным числом (при условии, что ее числитель делится на знаменатель без остатка).
Как смешанное число перевести в неправильную дробь
Вопрос о том, как перевести смешанное число в неправильную дробь, возникает как при умножении и делении смешанных чисел, так и в качестве самостоятельного задания.
Чтобы смешанное число перевести в неправильную дробь, надо:
1) Целую часть умножить на знаменатель и к произведению прибавить числитель. Результат записать в числитель.
2) Знаменатель переписать без изменения.
С помощью схемы перевод смешанного числа в неправильную дробь можно изобразить так:
Теперь рассмотрим, как смешанное число перевести в неправильную дробь, на конкретных примерах.
А как целое число записать в виде неправильной дроби? Для этого достаточно представить его в виде дроби, числитель которой равен данному числу, а знаменатель — единица. С помощью схемы перевод целого числа в неправильную дробь можно изобразить так:
Примеры записи целого числа в виде неправильной дроби:
38 Comments
СУПЕР САЙТ БОЛЬШОЕ СПАСИБО РАЗРАБОТЧИКАМ!Я ПОНЯЛ. КЛАССНЫЙ САЙТ.
Спасибо,очень помогли,всё доступно объяснили
Пожалуйста! ? Успехов Вам!
Meley! Желаю Вам дальнейших успехов в учебе!
Сайт просто супер всё понятно класс
классный сайт. отдельное большое спасибо всем разработчикам!!
Спасибо, Вова!
Я надеюсь, сайт поможет Вам освоить математику на «отлично».
супер-пупер спасибо большое я по математике получила 12 благодаря вам.
meley:
10.02.2014 в 15:23 (Изменить)
Светлана Иванова благодаря вам я стала отличницей и все у меня спрашивают в классе как ты стала отличницей а я говорю благодаря Светлане Ивановой