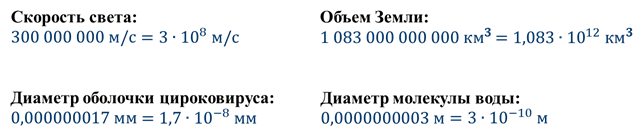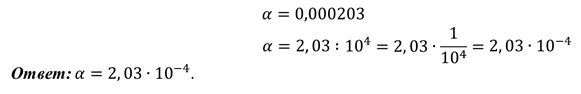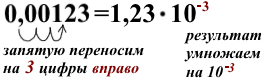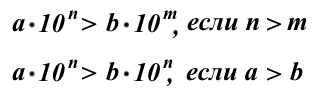Cтандартный вид числа
В задачах по физике часто приходится работать с очень большими и очень малыми величинами.
Как вести вычисления в атомной физике? Или записать радиус электрона? Если потребуется сравнить массу электрона и массу планеты Земля, как произвести вычисления с числами, которые несопоставимы друг с другом в обычном виде?
Физики и математики, столкнувшись с такими задачами, поняли, что для решения подобных задач требуется привести числа к единому стандартному виду. Так появилось понятие стандартный вид числа.
Прежде чем переходить к объяснению, как записать число в стандартном виде, нужно вспомнить определение степени. Особенно хорошо нужно помнить, чему равняется число « 10 » в различных степенях.
Вспомним, что при умножении целого числа на 10, 100, 1000 и т.д. мы просто добавляли тоже количество нулей, что и в 10, 100, 1000 и т.д..
Теперь запишем тоже самое, используя определение степени.
При делении целого числа на 10, 100, 1000 и т.д. мы убирали нули.
С помощью степени можно записать вычисления выше следующим образом:
С помощью определения отрицательной степени можно записать вычисления выше следующим образом:
Стандартный вид числа
Вначале обратимся к строгому математическому определению стандартного вида числа. Затем по традиции разберемся на примерах.
Любое натуральное число или конечную положительную десятичную дробь можно записать в виде:
Такая запись называется — стандартный вид числа.
При этом число « n » называют порядком числа « a ».
Теперь к примеру. Пусть нам дано число « 5 600 » и требуется записать его в стандартном виде.
По определению стандартного вида числа необходимо, чтобы перед запятой стояла только одна цифра от « 1 » до « 9 ».
В числе « 5 600 » первая цифра справа — « 5 ». Поставим справа от нее запятую и посчитаем, сколько знаков у нас осталось справа от запятой.
Теперь запишем « 1000 » с использованием степени.
Завершающим штрихом будет отбрасывание незначащих нулей в десятичной дроби.
Таким образом « 5 600 » в стандартном виде будет выглядеть следующим образом:
Чтобы проверить, что мы не ошиблись в вычислениях, произведем вычисления обратно. Если все выполнено корректно, мы должны получить изначальное число. Убедимся в этом.
Рассмотрим другой пример, когда нужно представить десятичную дробь в стандартном виде. Например, десятичную дробь « 0,017 ».
Согласно определению стандартного вида числа необходимо, чтобы первой цифрой перед запятой стояла только одна цифра от « 1 » до « 9 ».
В десятичной дроби « 0,017 » вначале идет « 0 ». Нам это не подходит, поэтому двигаемся слева направо, чтобы найти первую цифру отличную от « 0 ».
Это цифра « 1 ». Посчитаем сколько знаков (цифр) стояло от запятой до цифры « 1 », включая саму цифру « 1 ».
Получается два знака. Начнем записывать « 0,017 » в стандартном виде. Перенесем запятую и поставим ее справа от « 1 ».
Выходит, чтобы из « 1,7 » сделать 0,017 », нужно « 1,7 разделить на « 100 » (чтобы перенести запятую на два знака влево).
Запишем это деление на « 100 », используя обыкновенную дробь.
С помощью отрицательной степени запишем окончательный вид числа « 0,017 » в стандартном виде.
Примеры решения задач
на запись числа в стандартном виде
№ 237 Алимов 8 класс
(Устно) Определить порядок числа, выражающего значение физической константы:
1) масса покоя электрона
me = 9,1093897 · 10 −31
Напоминаем, что порядком числа, которое приведено в стандартный вид, называют степень, в которой стоит « 10 ». В данном примере « 10 » стоит в
степени « −31 ». Значит, порядком массы покоя электрона является « −31 ».
№ 238 Алимов 8 класс
2) постоянная Фарадея
F = 96485,309 Кл/моль;
По определению стандартного вида числа необходимо, чтобы перед запятой стояла только одна цифра от « 1 » до « 9 ».
Начнем записывать постоянную Фарадея в стандартном виде. Перенесем запятую после первой цифры отличной от нуля. Это цифра « 9 ».
Получается « 4 » знака. Значит постоянная Фарадея в стандартном виде будет выглядеть следующим образом:
Порядком числа « 9,6485309 · 10 4 » является степень, в которой стоит « 10 ». Следовательно, порядок « k = 4 ».
Начнем записывать постоянную Лошмидта в стандартном виде, т.е. как:
Завершим решение и запишем окончательный ответ, используя свойство «Произведение степеней».
Стандартный вид числа
В данной публикации мы рассмотрим, что такое стандартный вид числа, и как он записывается. Также разберем практические примеры по этой теме.
Запись больших и маленьких чисел
В точных науках время от времени встречаются очень большие или, наоборот, маленькие значения величин. Чтобы было комфортнее работать с ними, и тем более, одновременно использовать вместе в одних и тех же расчетах, был придуман некий общий принцип записи чисел, так называемый стандартный вид.
Чтобы в полной мере усвоить представленный ниже материал, необходимо знать, что такое степень. К примеру, продемонстрируем ее разные варианты на числе 10:
Также напомним, для того, чтобы какое-то число умножить на 10, 100, 1000, 10000 и т.д., мы просто приписываем к нему количество нулей, которое содержится в 10, 100, 1000, 10000 и т.д. Например,
То же самое касается и деления на 10, 100, 1000, 10000 и т.д., только здесь мы убираем нули:
Перечисленные выше действия можно представить в другом виде – как произведение на 10 в определенной степени:
Десятичные дроби
Если мы имеем дело с десятичным дробями, то в целом всё аналогично. При их умножении на 10, 100, 1000 и т.д. мы смещаем запятую-разделитель вправо на столько позиций, сколько нулей содержится в 10, 100, 1000 и т.д.
Если нужно разделить десятичную дробь на 10, 100, 1000 и т.д., то мы смещаем запятую влево на соответствующее нулям количество позиций:
Стандартный вид числа
Натуральное число или десятичную дробь (конечную) в общем виде можно представить следующим образом:
Такая запись и есть стандартный вид числа.
Пример 1
Представим число 2300 в стандартном виде.
Решение:
Первая цифра числа – это 2, она находится между нулем и десятью, что удовлетворяет условию выше.
Ставим после двойки запятую-разделитель и отсчитываем, сколько цифр у нас осталось после нее справа. В нашем случае их три.
Следовательно, мы умножаем полученную десятичную дробь ( a ) на число 10, степень которого равняется количеству цифр после запятой:
Другими словами, мы умножили дробь на 1000 (10 3 ).
Как мы знаем, в десятичной дроби нули в конце дробной части можно опустить, т.е. финальная запись числа 2300 в стандартном виде выглядит так:
Пример 2
Представим число 0,0029 в стандартном виде.
Решение:
Нам нужно, чтобы до запятой (т.е. слева от нее) стояла цифра от 1 до 9. Следовательно, перемещаем запятую на три позиции вправо.
Получаем новую десятичную дробь 2,9. Ее нужно умножить на 10, но в отрицательной степени, т.к. мы сделали число кратно больше исходного. Значение степени равняется количеству позиций, на которое была сдвинута запятая, т.е. в нашем случае получается “минус три”.
Стандартный вид числа
Урок 36. Алгебра 8 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Стандартный вид числа»
Наверняка, в физике, биологии, химии или географии вы сталкивались, как с очень большими, так и очень малыми положительными числами.
Скажите с такими числами удобно выполнять математические расчёты? Конечно же, нет. В обычном десятичном виде большие и малые числа неудобно читать и записывать, неудобно выполнять над ними какие-либо действия. В таком случае полезным оказывается представление числа в виде
Говорят, что мы записали числа в стандартном виде. В таком виде можно представить любое положительное число.
Стандартным видом числа 
называют его запись в виде: 
, где 
и 
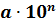
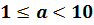
– целое число.
Число называется порядком числа .
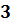
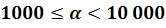
Если порядок числа равен 
, то это означает, что 
.
Если порядок числа равен 
, то это означает, что 
.
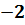
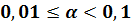
Большой положительный порядок показывает, что число очень велико.
Большой по модулю отрицательный порядок показывает, что число очень мало.
, где и – целое число
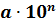
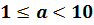
По определению стандартного вида числа следует, что в стандартном виде в целой части числа (до запятой) может содержаться только одна цифра.
Все остальные цифры должны стоять после (справа) от запятой.
Порядок числа даёт представление о том, насколько велико или мало это число.
В стандартном виде можно записать не только большое или малое, но и любое число.
Для того чтобы привести число к стандартному виду, надо:
1. Перенести в нём запятую так, чтобы она была сразу после первой значащей цифры.
2. полученное число умножить на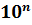 
, где подбирается так, чтобы произведение было равно данному числу.
Значащей цифрой числа называют его первую (слева направо) отличную от нуля цифру, а также все последующие за ней цифры.
Пример: представим в стандартном виде число.
Задание: запишите число в стандартном виде.
Задание: запишите в стандартном виде число, равное значению произведения х и у.
Стандартным видом числа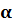 
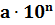
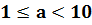
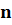
называют его запись в виде: 
, где 
и 
– целое число.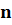
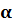
Число называется порядком числа .
Для того, чтобы привести число к стандартному виду, надо перенести в нём запятую так, чтобы она была сразу после первой значащей цифры, и полученное число умножить на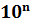 
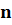
, где подбирается так, чтобы произведение было равно данному числу.
Стандартный вид числа
Что такое стандартный вид числа
В различных дисциплинах (таких как, физика, химия, география) приходится сталкиваться как с очень большими, так и с очень малыми величинами. В обычном десятичном виде большие и малые числа неудобно читать и записывать, неудобно выполнять над ними какие-либо действия. В таком случае полезным оказывается представление числа в так называемом стандартном виде. Числа в стандартном виде удобно применять для действий и измерений несопоставимых величин между собой (например, массы электрона и массы планеты Земля).
Как представить число в стандартном виде
Для того чтобы представить некоторое число в стандартном виде, необходимо представить его в виде произведения, первый множитель которого — число от 1 до 10 (не включая 10), второй — степень десяти. Для представления числа в стандартном виде необходимо вспомнить определение степени числа.
Степень некоторого числа — это результат умножения числа на само себя заданное количество раз.
Итак, чтобы записать число в стандартном виде, следует разделить его на такую степень десяти, чтобы результат находился между 1 (включительно) и 10 (не включая). Затем следует умножить его обратно на ту же степень десятки, записав ее в виде степени. Важный момент, исходя из определения стандартного числа, в таком виде мы можем представить только положительные числа, т.к. основание (мантисса) числа должна лежать в промежутке от 1 до 10 (не включительно), поэтому в дальнейшем будем говорить о стандартном виде положительного числа.
Сравнение чисел, записанных в стандартном виде
Для сравнения чисел необходимо сравнивать между собой порядки, а затем мантиссы чисел.
Выполнение операций над числами в стандартном виде
Над числами в стандартном виде можно проводить те же математические операции, что и над обычными числами, а именно:
Пояснение на примерах
Подведем итог, и разберем все вышеуказанные правила по работе с числами в стандартном виде на конкретных примерах.
Представление числа в стандартном виде
Записать в стандартном виде и определить порядок числа k, выражающего физического константу: постоянная Фарадея F = 96485,309 Кл/моль. Запишем решение, для этого заметим, что если перенести запятую на 4 знака влево, то получим число, лежащее в промежутке от 1 до 10, а именно 9,6484309.
Сравнение чисел в стандартном виде
Выполнение операций над числами в стандартном виде
Стандартный вид числа
Стандартный вид числа — это его запись в виде произведения
Число n называется порядком числа, записанного в стандартном виде.
В стандартном виде можно записать любое положительное число.
Как правило, стандартный вид числа используют для записи больших и малых величин.
Записать число в стандартном виде и указать порядок числа:
Чтобы записать число в стандартном виде, надо представить его в виде произведения, первый множитель которого — число от единицы до десяти (1≤a 
Получили число, записанное в стандартном виде. Его порядок n=6.
При решении примеров на приведение числа к стандартному виду удобнее деление числа на
заменить умножением на
Итак, для приведения к стандартному виду числа, больше либо равного 10, запятую в его записи переносим влево на n цифр и результат умножаем на 10 в степени n:
2) 12 346 000 000=12 346 000 000,
Чтобы величина первого множителя входила в промежуток от 1 до 10, надо запятую в записи данного числа перенести на 10 знаков влево, а чтобы число не изменилось, умножить результат на 10¹º:
Это число записано в стандартном виде. Его порядок n=10.
Чтобы первый множитель соответствовал условию 1≤a 
Число 5430 представляем в стандартном виде. Для этого запятую в его записи переносим на 3 цифры влево и результат умножаем на 10³.
Далее выполняем умножение степеней с одинаковыми основаниями.
Сравнение чисел, записанные в стандартном виде
9,8 \cdot 10^7 \]» title=»Rendered by QuickLaTeX.com»/>
так как порядок первого числа больше порядка второго числа (8>7);
поскольку порядок первого числа меньше порядка второго числа (-8 
2,97 \cdot 10^9 \]» title=»Rendered by QuickLaTeX.com»/>
так как при равных порядках первый множитель у первого числа больше, чем у второго (3,4>2,97).