Слово Как написать arctg в маткаде - однокоренные слова и морфемный разбор слова (приставка, корень, суффикс, окончание):

MathCAD. MatLab

И другие программы этой серии

MathCAD 2001

— Арктангенса нет на панелях инструментов, поэтому его нужно найти в специальном списке функций. Вызвать этот список можно либо сочетанием [Ctrl]+[E], либо выполнив команду Insert / Function (Вставка/Функция), либо при помощи специальной кнопки панели Standard (Стандартная). В открывшемся окне есть список категорий функций (Function Category), список самих функций выбранной категории (Function Name), а также окно информации о выбранной функции. По умолчанию определена категория All (Все) и в окне Function Name находится полный список всех встроенных функций MathCAD.
Очевидно, что арктангенс нужно искать в категории Trigonometric (Тригонометрические). Среди множества всевозможных тригонометрических функций находится 2 вида арктангенса (Atan и Atan2).
Для того чтобы определить, какой из них следует выбрать, прочитаем описание для каждого:
Atan(Z). \»Returns the angle (in radians) whose tangent is z. Principal value for complex z.\» \»Возвращает угол (в радианах), для которого тангенс — это Z. Главное значение для комплексного Z\».
Atan2(x,y). \»Returns the angle (in radians) from the x-axis to a line containing the origin (0, 0) and the point (x, y). Both x and y must be real.\» \» Возвращает угол (в радианах) между осью x и линией, содержащей точку начала координат и точку (x,y). X и Y должны быть действительными\».
Очевидно, нужно использовать первую функцию. Выбираем ее и нажимаем Ok.
2) Выражение введено, но параметры его вида, установленные по умолчанию, зачастую могут не удовлетворить пользователя. Для того чтобы отредактировать вид выражения, нужно при помощи команды Format/Equation (Формат/Уравнение) вызвать соответствующее меню.
Здесь вы можете определить цвет шрифта формул (Default equation color), выбрать стиль (Style name). При помощи кнопки Modify (Модифицировать) вы можете изменить стиль текста формул: выбрать тип, размер, начертание шрифта. Чтобы поменять параметры самой математической области, выполните правый щелчок мышью по любой точке редактируемой формулы и в открывшемся контекстном меню выберите пункт Properties (Свойства).

Источник

Как записать arccos в mathcad

Как записать sin в квадрате в mathcad

Система MathCAD содержит большой набор встроенных элементарных функций. Функции задаются своими именами и значениями аргумента, заключёнными в круглых скобках. Функции, как и переменные, и числа, могут входить в состав математических выражений. В ответ на обращение к ним, функции возвращают вычисленные значения. Ниже представлены некоторые из этих функций.

1.2.1 Тригонометрические функции

1.2.2 Гиперболические функции

sinh (z) — гиперболический синус
cosh(z) — гиперболический косинус
tanh(z) — гиперболический тангенс
sech(z) — гиперболический секанс
csch(z) — гиперболический косеканс
coth(z) — гиперболический котангенс

1.2.3 Обратные тригонометрические функции

asin (z) — арксинус
acos(z) — арккосинус
atan(z) — арктангенс

1.2.3 Обратные тригонометрические функции

asin (z) — арксинус
acos(z) — арккосинус
atan(z) — арктангенс

1.2.4 Обратные гиперболические функции

asinh (z) — обратный гиперболический синус
acosh(z) — обратный гиперболический косинус
atanh(z) — обратный гиперболический тангенс

1.2.5 Показательные и логарифмические функции

exp (z) — экспоненциальная функция
ln (z) — натуральный логарифм
log (z) — десятичный логарифм

1.2.6 Функции с условиями сравнения

ceil (x) — наименьшее целое, большее или равное х
floor(x) — наибольшее целое, меньшее или равное х
mod(x,y) — остаток отделения х/у со знаком х
angle(x,y) — положительный угол с осью х для точки с координатами (х,у)

Синус в квадрате X
Как собственно записать F(x)=sin^2\,x-cos\,2x Точнее сам синус в квадрате икс. Range(«B» &.

Построить график функции тангенс в квадрате
Нужно построить график функции тангенс в квадрате tan2(x). Помогите, у меня не получается. Вот мой.

Нарисовать квадрат в квадрате, в квадрате и так далее
Прошу помощи, мне подкинули задачку. Необходимо вывести на экран вот это: * * * * * * * * * *.

Найти сумму чисел 1 в квадрате до 10 в квадрате
Создать программу по всем 3 видам циклов. цикл с параметром,цикл с условием,цикл,и цикл с.

Найти сумму от N в квадрате, до 2N в квадрате
Дано N(>0) Найти сумму sqr(N)+sqr(N+1)+sqr(N+2)+. +sqr(2*N)

График, как задать синус в квадрате

Не могу построить график, пробовал вариант, заменяя выражение (выделеные) на sin(x) = sin(pi/6)(3-4t^2), все равно нечего не хочет работать. Может кто поможет или даст ссылку, где написано, как решить мою проблему, заранее спасибо.

Синус в квадрате X
Как собственно записать F(x)=sin^2\,x-cos\,2x Точнее сам синус в квадрате икс. Range(«B» &.

Построить график функции тангенс в квадрате
Нужно построить график функции тангенс в квадрате tan2(x). Помогите, у меня не получается. Вот мой.

Не работает ln^2(ln в квадрате)

Нарисовать квадрат в квадрате, в квадрате и так далее
Прошу помощи, мне подкинули задачку. Необходимо вывести на экран вот это: * * * * * * * * * *.

Найти сумму чисел 1 в квадрате до 10 в квадрате
Создать программу по всем 3 видам циклов. цикл с параметром,цикл с условием,цикл,и цикл с.

Найти сумму от N в квадрате, до 2N в квадрате
Дано N(>0) Найти сумму sqr(N)+sqr(N+1)+sqr(N+2)+. +sqr(2*N)

Х в квадрате
каким образом мжно делать что бы Х выводился на экарн со степенем?

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Синус в квадрате X
Как собственно записать F(x)=sin^2\,x-cos\,2x Точнее сам синус в квадрате икс. Range(«B» &.

Прямоугольник в квадрате
Здравствуйте,попал в очень неприятную ситуацию, понадеялся на человека, а он «не смог». Времени.

Жизнь в квадрате
В некоторых клетках квадрата N x N живут микроорганизмы (не более одного в одной клетке). Каждую.

Задача о квадрате
Есть у нас квадрат у него бросают 3 точки какая вероятность того что эти три точку образуют 1).

Источник

Как написать arctg в маткаде

Этот раздел описывает тригонометрические, гиперболические и показательные функции Mathcad вместе с обратными им. Здесь также описываются встроенные функции Бесселя.

Тригонометрические функции и обратные им.

Тригонометрические функции Mathcad и обратные им определены для любого комплексного аргумента. Они также возвращают комплексные значения везде, где необходимо. Результаты для комплексных значений вычисляются с использованием тождеств:

Для применения этих функций к каждому элементу вектора или матрицы используйте оператор векторизации.

Обратите внимание, что все эти тригонометрические функции используют аргумент, выраженный в радианах. Чтобы перейти к градусам, используется встроенная единица deg. Например, чтобы вычислить синус 45 градусов, введите sin(45*deg).

Имейте в виду, что из-за ошибок округления, свойственных машинной арифметике, Mathcad может возвращать очень большое число в той точке, где находится особенность вычисляемой функции. Вообще, необходимо быть осторожным при вычислениях в окрестности таких точек.

asin(z)	Возвращает угол (в радианах), чей синус — z.
acos(z)	Возвращает угол (в радианах), чей косинус — z.
atan(z)	Возвращает угол (в радианах), чей тангенс — z.

Гиперболические функции sinh и cosh определяются формулами:

Эти функции также могут использовать комплексный аргумент и возвращать комплексные значения. Гиперболические функции тесно связаны с тригонометрическими функциями. Справедливы формулы:

sinh(iz)=isin(z)cosh(iz)=cos(z)

sinh (z)	Возвращает гиперболический синус z.
cosh (z)	Возвращает гиперболический косинус z.
tanh (z)	Возвращает sinh(z)/cosh(z), гиперболический тангенс z.
csch (z)	Возвращает 1/sinh(z), гиперболический косеканс z.
sech (z)	Возвращает 1/cosh(z), гиперболический секанс z.
coth (z)	Возвращает 1/tanh(z), гиперболический котангенс z.
asinh (z)	Возвращает число, чей гиперболический синус — z.
acosh (z)	Возвращает число, чей гиперболический косинус — z.
atanh (z)	Возвращает число, чей гиперболический тангенс — z.

Логарифмические и показательные функции

Логарифмические и показательные функции Mathcad могут использовать комплексный аргумент и возвращать комплексные значения. Значения экспоненциальной функции для комплексного аргумента вычисляются с применением формулы

e x+iy =e x (cos(y) + isin(y))

Вообще говоря, значения натурального логарифма даются формулой

ln(x + iy)=ln|x + iy|+ atan(y/x)i + 2n p i

В Mathcad функция ln возвращает значение, соответствующее n = 0. А именно:

ln(x + iy)=ln|x + iy|+ atan(y/x)i

Оно называется основным значением логарифма. Рисунок 1 иллюстрирует некоторые основные свойства логарифма.

exp(z)	Возвращает e в степени z.
ln(z)	Возвращает натуральный логарифм z. (z0).
log(z)	Возвращает логарифм z по основанию 10. (z0).

На Рисунке 1 показано, как можно использовать эти функции для вычисления логарифма по любому основанию.

Рисунок 1: Использование логарифмических функций.

Эти функции обычно возникают как решения для волнового уравнения, подчиненного цилиндрическим граничным условиям.

Функции Бесселя первого и второго рода, J_n(x) и Y_n(x), являются решениями для дифференциального уравнения

Модифицированные функции Бесселя первого и второго рода, I_n(x) и K_n(x), являются решениями для немного видоизмененного уравнения:

J0(x)	Возвращает J0(x); x вещественный.
J1(x)	Возвращает J1(x); x вещественный.
Jn(m, x)	Возвращает Jn(x); x вещественный, 0m100.
Y0(x)	Возвращает Y0(x); x вещественный, x > 0.
Y1(x)	Возвращает Y1(x); x вещественный, x > 0.
Yn(m, x)	Возвращает Yn(x). x > 0, 0m100
I0(x)	Возвращает I0(x); x вещественный.
I1(x)	Возвращает I1(x); x вещественный.
In(m, x)	Возвращает In(x); x вещественный, 0m100.
K0(x)	Возвращает K0(x); x вещественный, x > 0.
K1(x)	Возвращает K1(x); x вещественный, x > 0.
Kn(m, x)	Возвращает Kn(x). x > 0, 0m100

Следующие функции возникают в широком круге задач.

x должен быть вещественным. G (z) Возвращает значение эйлеровой гамма-функции в z. Для вещественного z значения этой функции совпадают со следующим интегралом:

Гамма-функция Эйлера удовлетворяет рекуррентному соотношению

Откуда следует для положительных целых z:

Интеграл ошибок часто возникает в статистике. Он может также быть использован для определения дополнения интеграла ошибок по формуле:

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

Работа с формулами в PTC Mathcad

Как правило, пользователям приходится осуществлять в PTC Mathcad расчет формул, которые оформляются следующим образом:

Пример выполнения данного ряда функций можно увидеть на рисунке ниже:

Благодаря этой статье вы узнаете, как функции float и explicit упрощают редактирование формул в процессе работы с программным компонентом PTC Mathcad.

Первым делом нужно определиться с переменными, из которых собственно и состоит конкретная рабочая формула, присвоив им соответствующие численные значения:

После этого можно задать имя итоговой переменной и требуемое выражение:

Обычно панель рабочих символов изначально открывается при запуске системы PTC Mathcad. В противном случае её можно открыть самостоятельно, перейдя на вкладку Вид. Там необходимо будет отыскать специальную Панель инструментов и открыть еще одну вкладку под названием «Символьные». Теперь в строке выражения заданных инструментов достаточно будет выбрать команду explicit. Она автоматически присвоит буквенным параметрам требуемые значения формулы. После выполнения всех этих процедур на рабочем поле отобразится специальный оператор в виде курсора. Рядом высветится уже знакомое слово explicit.

Для грамотного расчета формулы нужно будет вручную ввести команду ALL через запятую от explicit. Она выступит в роли модификатора, который указывает на необходимость подстановки в формулу всех имеющихся переменных. После этого за пределами выражения команды нужно будет нажать левую клавишу мышки, чтобы получить результат расчета:

Если вы хотите задать конкретное число знаков после запятой, которое должно отобразиться на экране в результате расчетов, тогда через выражение с помощью курсора можно воспользоваться еще одной полезной функцией – float:

После соответствующей надписи в специально отведенном месте необходимо будет записать требуемое число десятичных разрядов. Таким образом, вы зададите точность расчетов, которая будет сохраняться при любых вычислениях и в случаях подстановки таких результатов в дальнейшие расчеты:

Теперь останется только спрятать ключевые слова и избавиться от стрелок, которые нужно будет в обязательном порядке заменить символами равенства. Аналогичные изменения должны также коснуться имеющихся операторов присваивания. Выделив требуемое выражение с помощью правой клавиши, достаточно будет запустить функцию «Отображать определение как» и в специальном разделе выбрать «Знак равенства», как видно из рисунка ниже:

Так непривычные операторы присваивания преобразятся и примут облик знакомого нам всем знака «равно»:

Теперь нужно будет зафиксировать выражение с вычислениями с помощью курсора и тоже задать «Знак равенства» в графе «Отображать вычисления как»:

Только на данном этапе расчета стрелки будут автоматически заменены традиционными знаками равенства:

Повторным нажатием правой клавиши в районе выражения вы сможете выполнить функцию «Скрыть ключевые слова»:

Данная процедура позволит пользователю спрятать лишние команды и функции из виду, чтобы привести формульные выражения к требуемому внешнему виду:

Если вы работаете с PTC Mathcad Prime, порядок подстановки значений в формульную функцию остается без изменений. Единственным недостатком такого программного средства является отсутствие возможности прятать ключевые слова команд и менять внешний вид операторов:

Источник

Как записать arctg в mathcad

Как записать arctg в mathcad

Смотрите определение. Котангенс определяется как отношение косинуса к синусу, или равносильное ctg(x) = 1/tg(x).

В маткаде котангенс выдаётся функцией cot() — посмотрите в разделе тригонометрических функций, она там есть.

1. У меня установлен МАТКАД 14 русская версия. Нажимаю «ВИД» «ПАНЕЛИ ИНСТРУМЕНТОВ» «КАЛЬКУЛЯТОР». В панели «калькулятор», котангенса «соt» — нет.

Полагаю, Вас ввело в недоумение следующее обстоятельство.
Дело в том, что в математич. анализе градусные меры углов практически не используют, а пользуются их естественной мерой — радианом.
Радиан безразмерен и нет нужды каждый раз таскать излишнее пояснение «рад.» перед соответствующими числовыми значениями — поэтому его обычно и не применяют, а пишут просто число.

Вот и в приведённом задании — числа 0,384; 0,48; 1,11; 1,48 — это величины углов в радианах, которые нужно выразить в градусах, минутах и секундах соответственно.
Перевод осуществляется довольно просто. Выше я уже упоминал какая связь между градусами и радианами:

Отсюда же следует что, например, углу в y (радиан) будет соответствовать градусная мера y·180°/π.
Подставляя вместо y первое из приведённых в задании чисел, а также
π≈3,1415926535
получаем, что ему будет соответствовать угол
y·180°/π ≈ 0,384·180°/3,1415926535 ≈ 22,001579°.

Дробную часть градусов следует перевести в минуты и секунды.
Зная, что 1°=60`, получаем что
0,001579° = 0,001579·60` = 0,09474`,
т.е. ноль полных минут.
Точно также, учтя 1`=60“, находим секунды:
0,09474` = 0,09474·60“ = 5,6844 ≈ 6“.

Полная выкладка:
y·180°/π ≈ 0,384·180°/3,1415926535 ≈ 22,001579° ≈ 22°6“.

Аналогично находятся градусные меры остальных углов.

это за число и что с ним делать непонятно? По калькулятору sin⁻¹ (0.5) = 30° градусам, а sin(30) = 0,5. По компьютеру это выглядит следующим образом.
Sin(π 30/180) = 0.5 asin(0.5) 180/π = 30

sin(0.5) = 0.479
означает что берётся синус от угла 0.5 (радиан).
В этом смысле МАТКАД произвёл расчёт верно.

№4 решить уравнение
27
а) x³ — 64x=0 б) x³ — 3x² — 3x + 9=0 в) x4(степени) — 3x² + — =0
16
№5

2x 2 7
а)_______________ — _______________ = __________
x² — 2x + 1 x³ — 2x² + x 3x² — x

1 1 1 1
б) ____________ — ________ = ________ — _______
x — 5 x — 7 x — 1 x — 3

На двух станках отштамповали 1800 деталей за 12ч.Известно,что 180 деталей на первом станке штампуют на 1ч быстрее,чем на втором.Сколько деталей в час штампуют на первом станке

sin(0.5) = 0.479
означает что берётся синус от угла 0.5 (радиан).
В этом смысле МАТКАД произвёл расчёт верно.

Как задать арктангенс в маткаде

Аргумент тригонометрических функций и результат обратных тригонометрических функций выражаются в радианах. Чтобы использовать значение угла в градусах, его необходимо перевести в радианы (листинг 10.6). Аргумент тригонометрических функций может быть комплексным.

Листинг 10.4. Примеры тригонометрических функций

Листинг 10.5. Примеры расчета угла между прямой и осью OX

Листинг 10.6. Расчет тригонометрических функций в градусах

Аргумент тригонометрических функций и результат обратных тригонометрических функций выражаются в радианах. Чтобы использовать значение угла в градусах, его необходимо перевести в радианы (листинг 10.6). Аргумент тригонометрических функций может быть комплексным.

Листинг 10.4. Примеры тригонометрических функций

Листинг 10.5. Примеры расчета угла между прямой и осью OX

Листинг 10.6. Расчет тригонометрических функций в градусах

Когда тот или иной физик использует понятие «физический вакуум», он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.

Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.

Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование «моря» двух компенсирующих друг друга энергий в вакууме — положительной и отрицательной, а также «моря» компенсирующих друг друга частиц — виртуальных (то есть кажущихся) электронов и позитронов в вакууме.

Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом — присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.

БАЗОВЫЕ ОПЕРАЦИИ.
РАНЖИРОВАННЫЕ ПЕРЕМЕННЫЕ. ФУНКЦИИ. ГРАФИКИ
МАССИВЫ

1 Запуск. Формульные и текстовые области

Запуск Mathcad: Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).

Документ Mathcad просматривается, интерпретируется и выполняется слева направо и сверху вниз и может включать три вида областей:

Для ввода математических символов: View / Toolbars / Math (Вид / Панели инструментов / Математическая).

Каждое математическое выражение набирается в отдельной формульной области. Одна формула – одна область!

Перемещение курсора — клавиша Пробел. Изменение направления уголка — клавиша Insert (Ins).

«:=» — «присвоить» — задать выражение (число или формулу)

«=» — «вычислить» подсчитать и вывести значение выражения.

Для вставки в документ текстовой области выполняют Insert / Text Region (Вставка / Область текста), либо просто нажимают в формульной области Пробел. Текстовая область имеет рамку с маркерами, позволяющими изменять ее размеры, и курсор в виде вертикальной линии красного цвета.

2 Ранжированные переменные. Функции. Графики

В Mathcad существует тип переменных, принимающих не одно, а множество значений. Такие переменные носят название ранжированных или дискретных. Ранжированная переменная – переменная, которая принимает ряд значений при каждом ее использовании, причем каждое значение отличается от соседнего на постоянную величину, называемую шагом.

Ранжированная переменная общего вида определяется выражением:

Здесь Имя – задаваемое пользователем имя ранжированной переменной;
x1 – первое значение ранжированной переменной;
x2 – второе значение ранжированной переменной (x2 = x1 + Dx — первое значение плюс шаг);
xn – последнее значение ранжированной переменной.
Значения x1 и x2 разделяются запятой, двоеточие представляет собой единый оператор, указывающий на изменение переменной в заданных пределах. Он вводится с клавиатуры клавишей «;» или выбирается с палитры математических инструментов Matrix (Векторы и матрицы) (кнопка — Range Variable).

Шаг изменения значений ранжированной переменной в явном виде обычно не задается, он определяется как x2 – x1.

Функции в системе Mathcad можно условно разделить на две группы: встроенные и функции пользователя. Встроенные функции изначально заданы в системе разработчиками. Имя функции вводится с клавиатуры, обычно в нижнем регистре. Полный перечень встроенных функций можно получить, выполнив команду Function (Функция) главного меню Insert (Вставка), или нажав на кнопку панели инструментов. При этом появляется окно, где справа перечислены возможные категории функций, а слева – список функций из выделенной категории.

Среди наиболее часто используемых функций можно указать:

Функция пользователя сначала должна быть определена, а затем к ней можно обращаться при вычислениях, записи алгебраических выражений, построении графиков и т. п. Функция пользователя определяется

Имя(список аргументов) := Выражение

Сначала задается имя функции, в круглых скобках указывается список аргументов функции (перечень используемых переменных), разделяемых запятыми. Затем вводится оператор присваивания. Справа от него записывается выражение, содержащее доступные системе операторы, операнды и функции с аргументами, указанными в списке аргументов.

Обращение к функции осуществляется по ее имени с подстановкой на место аргументов констант, переменных, определенных до обращения к функции, и выражений.

Основные виды графиков и инструменты для работы с ними находятся на палитре математических инструментов Graph (График).

Для построения графика функции одной переменной в декартовой системе координат в Mathcad:

Примечание — Для построения в одной координатной плоскости графиков двух и более функций их имена или определяющие выражения перечисляются в знакоместе по оси ординат через запятую.

Массив в пакете Mathcad – это совокупность конечного числа упорядоченных пронумерованных элементов, которая может иметь уникальное имя. Обычно используют одномерные (векторы) и двумерные (матрицы) массивы, содержащие числовые, символьные или строковые данные.

Порядковый номер элемента называется индексом. Местоположение элемента в массиве задается одним индексом для вектора и двумя – для матрицы. Номер первого элемента массива определяется значением системной переменной ORIGIN. По умолчанию ORIGIN = 0 и может принимать только целые значения. Изменение значения этой системной переменной осуществляется последовательностью команд Math / Options… / Built-In Variables / Array Origin (ORIGIN) (Математика / Параметры / Встроенные переменные / Начальный индекс массивов) или переопределением в документе, например:

Существует несколько способов создания массивов.

1-й способ. Использование панели Matrix (Матрицы).

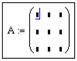
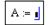
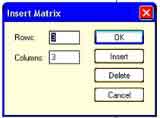
Сначала набирается имя массива и оператор присваивания, например, . Далее на панели Math (Математика) выбираем кнопку Matrix (Матриц):

Далее указываем количество ее строк m (Rows) и столбцов n (Columns) матрицы. Для векторов один из этих параметров должен быть равен 1. При m = 1 получим вектор-строку, а при n = 1 – вектор-столбец.

На месте курсора появится шаблон, в знакоместа которого вводятся значения элементов массива:

2-й способ. Использование ранжированной переменной.

Целочисленные ранжированные переменные используются для задания индексов и позволяют создавать массивы в следующем порядке:

Обращаться к отдельным элементам вектора или матрицы можно, используя нижний индекс, принимающий только целочисленные значения. Для ввода нижнего индекса после имени вектора или матрицы нажимается клавиша «[» (прямая открывающая скобка) либо используется пиктограмма 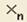с палитры математических инструментов Matrix. Для элемента матрицы указываются через запятую два индекса, обозначающих номер строки и номер столбца соответственно.

Для работы с векторами и матрицами система Mathcad имеет ряд специальных операторов и команд (представленных в таблице 1), используя которые не следует забывать об общих правилах матричного исчисления.

Таблица 1 – Команды палитры инструментов Matrix (Матрица)

Источник