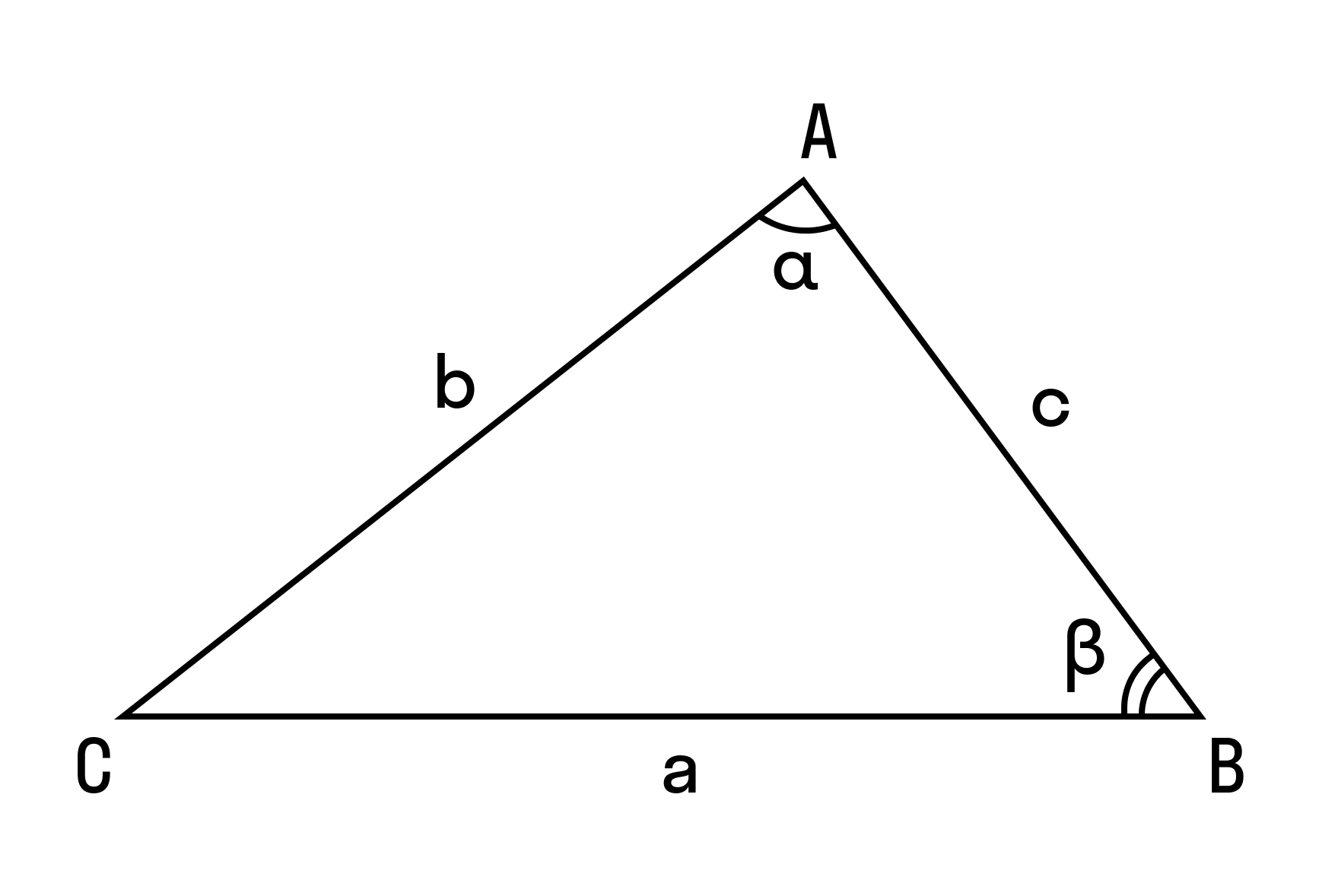
Теорема косинусов и синусов
Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула Теоремы Пифагора:
a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.
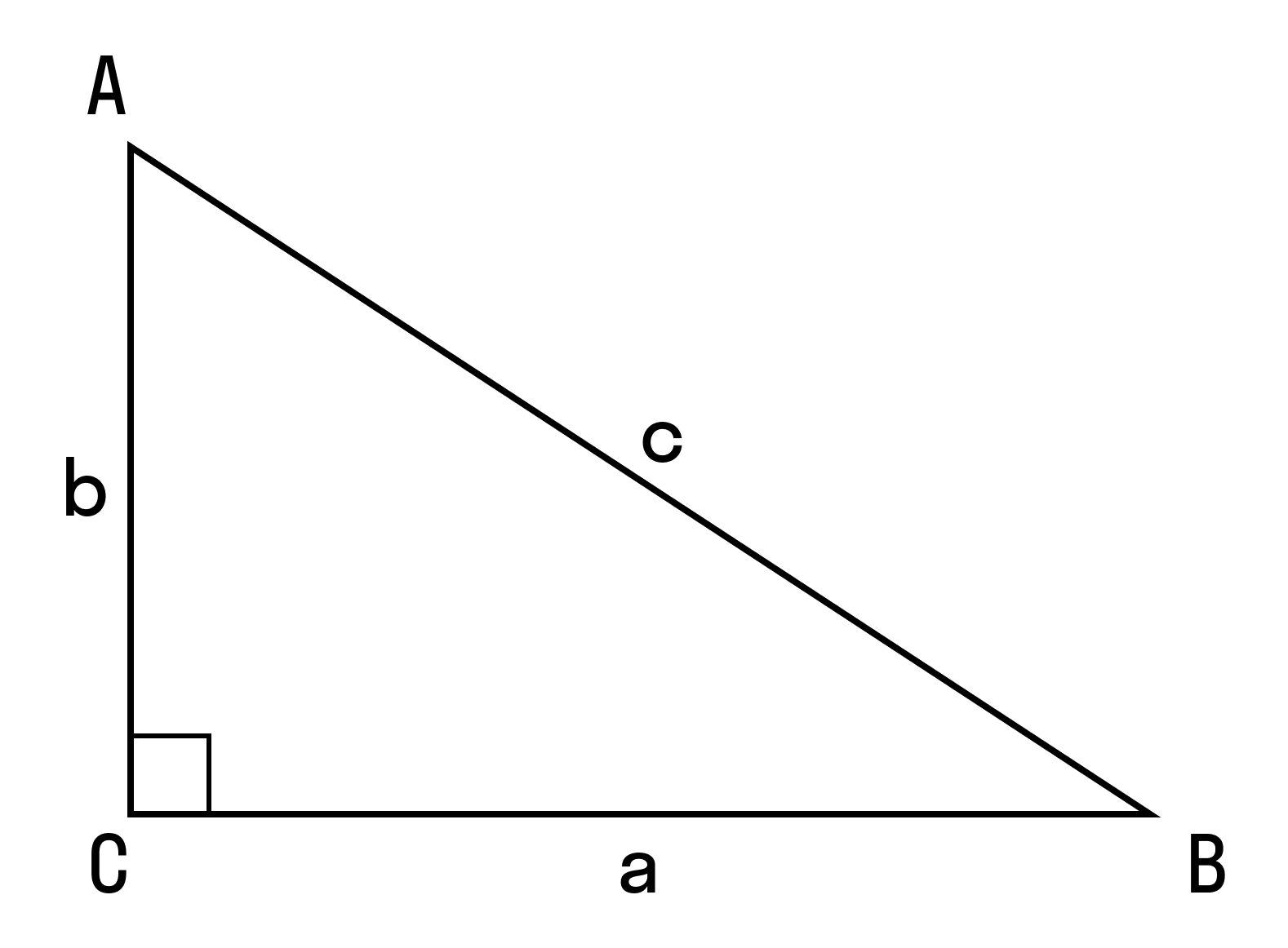
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.
Что и требовалось доказать.
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.
С помощью теоремы косинусов можно найти косинус угла треугольника:
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
Приравниваем правые части уравнений:
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
Теорема косинусов может быть использована для любого вида треугольника.
Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
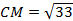
Теорема косинусов
Теорема косинусов — в любом треугольнике квадрат одной стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих двух сторон на косинус угла между ними.
Например:
Одна сторона треугольника равна 12 см, другая — 8 см, между ними образовался угол 120º. Найдите длину третьей стороны.
Решение по формуле a² = b² + c² – 2b.c.cosα:
Длина третьей стороны — примерно 17,436 см.
Следствия
Следствие косинуса угла треугольника
При помощи теоремы косинусов можно найти косинус угла треугольника.
Используйте теорему косинусов, чтобы найти угол β.
Решение:
Будем использовать эту версию формулы:
cos β = (6² + 8² − 7²) / 2×6×8
Следствие верхней части формулы cos α
Чтобы узнать, если угол α острый, прямой или тупой, нужно вычислить b²+c²−a² (это верхняя часть формулы для cos α):
Доказательство теоремы косинусов
Нужно доказать, что c² = a² + b² − 2a.b.cos C
1. Из определения косинуса известно, что в прямоугольном треугольнике BCD: cos C = CD/a CD = a.cos C.
2. Вычитаем это из стороны b, так мы получим DA:
3. Мы знаем из определения синуса, что в том же треугольнике BCD:
sin C = BD/a BD = a.sinC.
4. Применяем теорему Пифагора в треугольнике ADB: c² = BD² + DA²
5. Заменим BD и DA из пунктов 2) и 3), получится выражение: c²= (a. sin C)²+(b−a.cos C)²
6. Раскрываем скобки: c² = a² sin ²C + b² − 2a.b.cosC + a².cos²C
6.1. Поменяем их местами (a²cos²C поставим на второе место): c² = a² sin ²C + a²cos²C + b² − 2a.b.cosC
7. Выносим за скобки «a²»: c² = a² (sin²C+cos²C) + b² − 2a.b.cosC
8. В скобках получилось основное тригонометрическим тождество (sin²α + cos²α = 1), значит его можно сократить т. к. умножение на единицу ничего не меняет, получилось: c² = a² + b² − 2a.b.cos C
Теорема косинусов для равнобедренного треугольника
В равнобедренном треугольнике:
Используем формулу теоремы косинусов
Подставляем все известные:
x² = 8² + 8² – 2×8×8×cos140º
x² = 64 + 64 – 128 × (-0,766)
Теорема синусов
Теорема синусов гласит, что отношение стороны треугольника к синусу угла, противолежащего данной стороне, одинаково для всех сторон и углов в данном треугольнике:
Теорема косинусов (ЕГЭ 2022)
Что же такое теорема косинусов?
Представь себе, это такая… теорема Пифагора для произвольного треугольника. Она однажды тебя спасёт!
Дальше смотри рисунки и ты все поймешь. Один рисунок лучше тысячи слов ?
Разберёшься в ней – будь уверен, что любая задача с треугольником окажется тебе под силу!
Теорема косинусов — коротко о главном
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Почему теорема косинусов это… теорема Пифагора
И причем тут теорема Пифагора? Сейчас поясню.
Согласно теореме Пифагора в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов.
А что будет, если угол \( \displaystyle \angle C\), скажем, острый?
Вроде ясно, что величина \( \displaystyle <
А если угол \( \displaystyle \angle C\) – тупой?
Ну, тогда величина \( \displaystyle <
Но, опять же, на сколько? И как это связано с величиной \( \displaystyle \angle C\)?
Обрати внимание на вот эту добавку к теорему Пифагора: \( \displaystyle «-2ab\cos \gamma »\).
Вот она и «адаптирует» теорему Пифагора под острые и тупые углы треугольника. Сейчас мы докажем теорему косинусов и ты увидишь в теореме косинусов теорему Пифагора своими глазами.
Доказательство теоремы косинусов
Итак, для всякого (и остроугольного, и тупоугольного и даже прямоугольного!) треугольника верна теорема косинусов.
Теорема косинусов гласит: квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
Рассмотрим три случая:
И убедимся, что для всех трех случаев теорема косинусов работает!
Угол С острый
\( \displaystyle \angle C
Он прямоугольный, можно пользоваться теоремой Пифагора:
\( \displaystyle AH\) можно выразить из треугольника (прямоугольного!) \( \displaystyle AHC\).
\( \displaystyle AH=b\sin \gamma \)
А вот \( \displaystyle BH=a-CH=a-b\cos \gamma \) (снова из \( \displaystyle \Delta AHC\) ).
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Угол С тупой
Начинаем точно также: опускаем высоту из точки \( \displaystyle A\).
А теперь, внимание, отличие!
\( \displaystyle BH=a+b\cos \left( <<180>^<\circ >>-\gamma \right)\).
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Угол С прямой
Но тогда \( \displaystyle \cos \gamma =0\) и теорема косинусов просто превращается в теорему Пифагора:
В каких же задачах бывает полезна теорема косинусов?
Ну, например, если у тебя даны две стороны треугольника и угол между ними, то ты прямо сразу можешь найти третью сторону.
Или, если тебе даны все три стороны, то ты тут же найдешь косинус любого угла по формуле:
И даже, если тебе даны две стороны и угол НЕ между ними, то третью сторону тоже можно найти, решая квадратное уравнение. Правда, в этом случае получается иногда два ответа и нужно соображать, какой же из них выбрать, или оставить оба.
Попробуй применять и не бояться – теорема косинусов почти также легка в обращении, как и теорема Пифагора.
И приходи к нам на бесплатные вебинары и занятия ( о них ниже).
Бонус: Вебинар на решение задач по теореме косинусов и синусов
Теорема косинусов (и синусов) — универсальный инструмент при решении треугольников — это теоремы косинусов и синусов.
А как мы уже знаем, почти любая задача в планиметрии сводится именно к треугольникам.
Этот вебинар из нашего курса подготовки к ЕГЭ по математике (о нем ниже). Вы выучите сами теоремы и научитесь применять их при решении задач первой части.
Берите ручку и бумагу и решайте вместе с Алексеем Шевчуком.
Теорема косинусов. Доказательство
Теорема 1 (теорема косинусов). Квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
То есть для любого треугольника ABC со сторонами a, b, c справедливо равенство:
Доказательство. Пусть задан треугольник ABC. Проведем высоту h из вершины C на сторону c=AB (Рис.1).
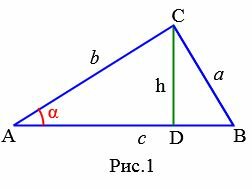 |
Теорема Пифагора для прямоугольных треугольников ADC и CDB имеет вид:
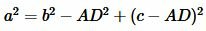 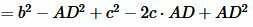 |
Учитывая, что: 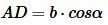
Доказательство (по векторам). Пусть задан треугольник ABC. Представим вектор AC в виде суммы векторов AB и BC (Рис.2).
где 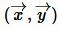
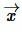
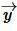
Используя дистрибутивность скалярного произведения векторов относительно сложения и коммутативность скалярного произведения векторов уравнение (5) можно преобразовать так:
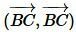 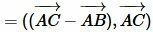 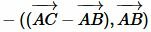 |
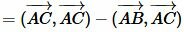 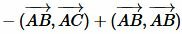 |
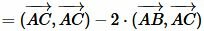 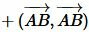 |
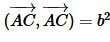 , , 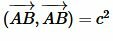 , , 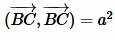 , , 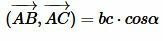 , , |
Примеры и решения
Задание 1. В треугольнике ABC, a=16, b=10, угол между ними 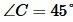
Решение. Из теоремы косинусов, имеем:
Подставляя значения сторон a, b и угла C в (6), получим:
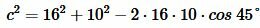 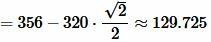 , , |
Ответ: 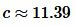
Задание 2. В треугольнике ABC, a=8, b=14, c=12. Найти углы α, β, γ (Рис.3).
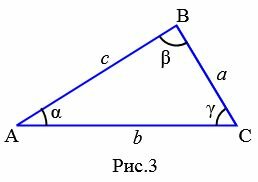 |
Решение. Из теоремы косинусов, имеем:
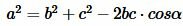 |
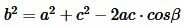 |
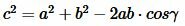 |
Подставляя значения a, b, c в (7), (8), (9), получим:
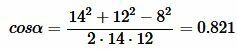 , , 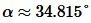 , , |
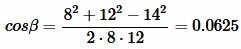 , , 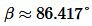 , , |
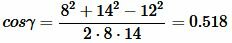 , , 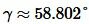 . . |
Ответ: 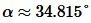
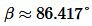
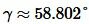
Теорема косинусов
Теорема косинусов — в любом треугольнике квадрат одной стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих двух сторон на косинус угла между ними.
Например:
Одна сторона треугольника равна 12 см, другая — 8 см, между ними образовался угол 120º. Найдите длину третьей стороны.
Решение по формуле a² = b² + c² – 2b.c.cosα:
Длина третьей стороны — примерно 17,436 см.
Следствия
Следствие косинуса угла треугольника
При помощи теоремы косинусов можно найти косинус угла треугольника.
Используйте теорему косинусов, чтобы найти угол β.
Решение:
Будем использовать эту версию формулы:
cos β = (6² + 8² − 7²) / 2×6×8
Следствие верхней части формулы cos α
Чтобы узнать, если угол α острый, прямой или тупой, нужно вычислить b²+c²−a² (это верхняя часть формулы для cos α):
Доказательство теоремы косинусов
Нужно доказать, что c² = a² + b² − 2a.b.cos C
1. Из определения косинуса известно, что в прямоугольном треугольнике BCD: cos C = CD/a CD = a.cos C.
2. Вычитаем это из стороны b, так мы получим DA:
3. Мы знаем из определения синуса, что в том же треугольнике BCD:
sin C = BD/a BD = a.sinC.
4. Применяем теорему Пифагора в треугольнике ADB: c² = BD² + DA²
5. Заменим BD и DA из пунктов 2) и 3), получится выражение: c²= (a. sin C)²+(b−a.cos C)²
6. Раскрываем скобки: c² = a² sin ²C + b² − 2a.b.cosC + a².cos²C
6.1. Поменяем их местами (a²cos²C поставим на второе место): c² = a² sin ²C + a²cos²C + b² − 2a.b.cosC
7. Выносим за скобки «a²»: c² = a² (sin²C+cos²C) + b² − 2a.b.cosC
8. В скобках получилось основное тригонометрическим тождество (sin²α + cos²α = 1), значит его можно сократить т. к. умножение на единицу ничего не меняет, получилось: c² = a² + b² − 2a.b.cos C
Теорема косинусов для равнобедренного треугольника
В равнобедренном треугольнике:
Используем формулу теоремы косинусов
Подставляем все известные:
x² = 8² + 8² – 2×8×8×cos140º
x² = 64 + 64 – 128 × (-0,766)
Теорема синусов
Теорема синусов гласит, что отношение стороны треугольника к синусу угла, противолежащего данной стороне, одинаково для всех сторон и углов в данном треугольнике: