Сумма и произведение цифр числа
Одной из часто используемых задач для начинающих изучать программирование является нахождение суммы и произведения цифр числа. Число может вводиться с клавиатуры или генерироваться случайное число. Задача формулируется так:
Дано число. Найти сумму и произведение его цифр.
Например, сумма цифр числа 253 равна 10-ти, так как 2 + 5 + 3 = 10. Произведение цифр числа 253 равно 30-ти, так как 2 * 5 * 3 = 30.
Обычно предполагается, что данная задача должна быть решена арифметическим способом. То есть с заданным число должны производиться определенные арифметические действия, позволяющие извлечь из него все цифры, затем сложить их и перемножить.
И здесь на помощь приходят операции деления нацело и нахождения остатка. Если число разделить нацело на 10, произойдет «потеря» последней цифры числа. Например, 253 ÷ 10 = 25 (остаток 3). С другой стороны, эта потерянная цифра есть остаток от деления. Получив эту цифру, мы можем добавить ее к сумме цифр и умножить на нее произведение цифр числа.
Пусть n – само число, suma – сумма его цифр, а mult – произведение. Тогда алгоритм нахождения суммы и произведения цифр можно словесно описать так:
Код программы на языке Python
Изменение значений переменных можно записать в сокращенном виде:
Приведенная выше программа подходит только для нахождения суммы и произведения цифр натуральных чисел, то есть целых чисел больше нуля. Если исходное число может быть любым целым, следует учесть обработку отрицательных чисел и нуля.
Если число отрицательное, это не влияет на сумму его цифр. В таком случае достаточно будет использовать встроенную в Python функции abc(), которая возвращает абсолютное значение переданного ей аргумента. Она превратит отрицательное число в положительное, и цикл while с его условием n > 0 будет работать как и прежде.
Программа, обрабатывающая все целые числа, может начинаться так:
Заметим, если в самом числе встречается цифра 0 (например, 503), то произведение всех цифр будет равно нулю. Усложним задачу:
Вводится натуральное число. Найти сумму и произведение цифр, из которых состоит это число. При этом если в числе встречается цифра 0, то ее не надо учитывать при нахождении произведения.
Для решения такой задачи в цикл добавляется проверка извлеченной цифры на ее неравенство нулю. Делать это надо до умножения на нее значения переменной-произведения.
Приведенный выше математический алгоритм нахождения суммы и произведения цифр числа можно назвать классическим, или универсальным. Подобным способом задачу можно решить на всех императивных языках, независимо от богатства их инструментария. Однако средства языка программирования могут позволить решить задачу другим, зачастую более простым, путем. Например, в Python можно не преобразовывать введенную строку с числу, а извлекать из нее отдельные символы, которые преобразовывать к целочисленному типу int:
Если добавить в код проверку, что извлеченный символ строки действительно является цифрой, то программа станет более универсальной. С ее помощью можно будет считать не только сумму и произведение цифр целых чисел, но и вещественных, а также цифр, извлекаемых из произвольной строки.
Строковый метод isdigit() проверяет, состоит ли строка только из цифр. В нашем случае роль строки играет одиночный, извлеченный на текущей итерации цикла, символ.
Глубокое знание языка Python позволяет решить задачу более экзотическими способами:
Встроенная функция sum() считает сумму элементов переданного ей аргумента.
Функция sum() в Python: питонический способ суммирования значений
Давайте разберем, что такое функция sum() в Python и почему это питонический способ суммирования.
Встроенная функция sum() – это эффективный и питонический способ суммирования списка числовых значений. Сложение нескольких чисел является обычным промежуточным шагом во многих вычислениях, поэтому sum() – довольно удобный инструмент для программиста Python.
Еще с помощью sum() можно объединять списки и кортежи. Это интересный дополнительный вариант использования, полезный, когда вам нужно сгладить список списков.
Приведенная ниже информация поможет вам эффективно решать проблемы суммирования в вашем коде с помощью sum() или других альтернативных и специализированных инструментов.
Понимание проблемы суммирования
Суммирование числовых значений – довольно распространенная задача в программировании. Например, предположим, что у вас есть список чисел a = [1, 2, 3, 4, 5] и вы хотите сложить элементы и получить сумму. Используя стандартную арифметику, вы сделаете что-то вроде этого:
Что касается математики, это выражение довольно простое.
Можно выполнить этот конкретный расчет вручную, но представьте себе другие ситуации, в которых это может быть невозможно. Если у вас очень длинный список чисел, добавление вручную будет неэффективным и, скорее всего, вы допустите ошибку. А если вы даже не знаете, сколько элементов в списке? Наконец, представьте сценарий, в котором количество элементов, которые вам нужно добавить, изменяется динамически или вообще непредсказуемо.
В подобных ситуациях, независимо от того, есть ли у вас длинный или короткий список чисел, Python может быть весьма полезен для решения задач суммирования.
Использование цикла for
Если вы хотите суммировать числа, создав собственное решение с нуля, вы можете использовать цикл for :
Здесь вы сначала инициализируете сумму и приравниваете её к 0. Эта переменная работает как аккумулятор, в котором вы сохраняете промежуточные результаты, пока не получите окончательный. Цикл перебирает числа и обновляет общее количество.
Цикл for можно заключить в функцию. Благодаря этому вы сможете повторно использовать код для разных списков:
В sum_numbers() вы берете итерируемый объект в качестве аргумента и возвращаете общую сумму значений элементов списка.
Использование рекурсии
Вы также можете использовать рекурсию вместо итерации. Рекурсия – это метод функционального программирования, при котором функция вызывается в пределах ее собственного определения. Другими словами, рекурсивная функция вызывает сама себя в цикле:
Когда вы определяете рекурсивную функцию, вы рискуете попасть в бесконечный цикл. Чтобы предотвратить это, нужно определить как базовый случай, останавливающий рекурсию, так и рекурсивный случай для вызова функции и запуска неявного цикла.
В приведенном выше примере базовый случай подразумевает, что сумма списка нулевой длины равна 0. Рекурсивный случай подразумевает, что общая сумма – это первый элемент плюс сумма остальных элементов. Поскольку рекурсивный случай использует более короткую последовательность на каждой итерации, вы ожидаете столкнуться с базовым случаем, когда числа представляют собой список нулевой длины.
Марк Лутц «Изучаем Python»
Скачивайте книгу у нас в телеграм
Использование reduce()
Вы можете вызвать reduce() с folding-функцией и итерируемым объектом в качестве аргументов. reduce() использует переданную функцию для обработки итерируемого объекта и вернет единственное кумулятивное значение.
Во втором примере folding-функция – это лямбда-функция, которая возвращает сложение двух чисел.
Поскольку суммирование является обычным явлением в программировании, писать новую функцию каждый раз, когда нам нужно сложить какие-нибудь числа, — бессмысленная работа. Кроме того, использование reduce() – далеко не самое удобочитаемое решение.
Начало работы с sum()
В настоящее время функция sum() является предпочтительным способом для суммирования элементов:
У sum() есть два аргумента:
Суммирование числовых значений
Вот несколько примеров использования sum() со значениями разных числовых типов:
Объединение последовательностей
Несмотря на то, что функция sum() в основном предназначена для работы с числовыми значениями, вы также можете использовать ее для объединения последовательностей, таких как списки и кортежи. Для этого вам нужно указать соответствующее значение для аргумента start :
Примеры использования sum() в Python
Кроме того, мы разберем, как применять sum() при работе со списками и кортежами. Мы также рассмотрим особый пример, когда нужно объединить несколько списков.
Расчет среднего значения выборки
Один из практических вариантов применения sum() – использовать ее в качестве промежуточного вычисления перед дальнейшими вычислениями. Например, вам нужно вычислить среднее арифметическое для выборки числовых значений. Среднее арифметическое, также известное как среднее значение, представляет собой общую сумму значений, деленную на количество значений в выборке.
Если у вас есть выборка [2, 3, 4, 2, 3, 6, 4, 2] и вы хотите вычислить среднее арифметическое вручную, вы можете решить эту операцию так:
(2 + 3 + 4 + 2 + 3 + 6 + 4 + 2) / 8 = 3,25
Нахождение скалярного произведения двух последовательностей
1 × 4 + 2 × 5 + 3 × 6 = 32
Чтобы извлечь последовательные пары значений, мы можем использовать zip(). Затем воспользуемся генератором для умножения каждой пары значений. Наконец, sum() поможет суммировать произведения:
Объединение списков
Но можно ли использовать функцию sum() для объединения списков, как в примере выше? Да! Вот как:
Это было быстро! Одна строка кода — и мы получили единый список. Однако использование sum() не кажется самым быстрым решением.
Важным недостатком любого решения, предполагающего конкатенацию, является то, что за кулисами каждый промежуточный шаг создает новый список. Это может быть довольно расточительным с точки зрения использования памяти.
Список, который в итоге возвращается, является самым последним созданным списком из всех, которые создавались на каждом этапе конкатенации. Использование генератора списка вместо этого гарантирует, что вы создадите и вернете только один список:
Эта новая версия flatten_list() более эффективна и менее расточительна с точки зрения использования памяти. Однако вложенные генераторы могут быть сложными для чтения и понимания.
Альтернативы sum()
Суммирование чисел с плавающей запятой: math.fsum()
Согласно документации, fsum() «позволяет избежать потери точности, отслеживая несколько промежуточных частичных сумм». В документации приводится следующий пример:
В этих примерах обе функции возвращают одинаковый результат. Это связано с невозможностью точного представления значений 0,1 и 0,2 в двоичной системе с плавающей запятой:
Объединение объектов с помощью itertools.chain()
chain() также является хорошим вариантом для объединения списков в Python:
Объединение строк с помощью str.join()
Заключение
Итак, сегодня мы разобрали, что такое функция sum() в Python. Теперь вы можете использовать её для сложения числовых значений. Эта функция обеспечивает эффективный, читаемый и питонический способ решения задач сложения в коде. Также мы поговорили про альтернативы функции sum() и в каких случаях их лучше использовать.
Сумма и произведение цифр числа
Одной из часто используемых задач для начинающих изучать программирование является нахождение суммы и произведения цифр числа. Число может вводиться с клавиатуры или генерироваться случайное число. Задача формулируется так:
Дано число. Найти сумму и произведение его цифр.
Например, сумма цифр числа 253 равна 10-ти, так как 2 + 5 + 3 = 10. Произведение цифр числа 253 равно 30-ти, так как 2 * 5 * 3 = 30.
Обычно предполагается, что данная задача должна быть решена арифметическим способом. То есть с заданным число должны производиться определенные арифметические действия, позволяющие извлечь из него все цифры, затем сложить их и перемножить.
И здесь на помощь приходят операции деления нацело и нахождения остатка. Если число разделить нацело на 10, произойдет «потеря» последней цифры числа. Например, 253 ÷ 10 = 25 (остаток 3). С другой стороны, эта потерянная цифра есть остаток от деления. Получив эту цифру, мы можем добавить ее к сумме цифр и умножить на нее произведение цифр числа.
Пусть n – само число, suma – сумма его цифр, а mult – произведение. Тогда алгоритм нахождения суммы и произведения цифр можно словесно описать так:
Код программы на языке Python
Изменение значений переменных можно записать в сокращенном виде:
Приведенная выше программа подходит только для нахождения суммы и произведения цифр натуральных чисел, то есть целых чисел больше нуля. Если исходное число может быть любым целым, следует учесть обработку отрицательных чисел и нуля.
Если число отрицательное, это не влияет на сумму его цифр. В таком случае достаточно будет использовать встроенную в Python функции abc(), которая возвращает абсолютное значение переданного ей аргумента. Она превратит отрицательное число в положительное, и цикл while с его условием n > 0 будет работать как и прежде.
Программа, обрабатывающая все целые числа, может начинаться так:
Заметим, если в самом числе встречается цифра 0 (например, 503), то произведение всех цифр будет равно нулю. Усложним задачу:
Вводится натуральное число. Найти сумму и произведение цифр, из которых состоит это число. При этом если в числе встречается цифра 0, то ее не надо учитывать при нахождении произведения.
Для решения такой задачи в цикл добавляется проверка извлеченной цифры на ее неравенство нулю. Делать это надо до умножения на нее значения переменной-произведения.
Приведенный выше математический алгоритм нахождения суммы и произведения цифр числа можно назвать классическим, или универсальным. Подобным способом задачу можно решить на всех императивных языках, независимо от богатства их инструментария. Однако средства языка программирования могут позволить решить задачу другим, зачастую более простым, путем. Например, в Python можно не преобразовывать введенную строку с числу, а извлекать из нее отдельные символы, которые преобразовывать к целочисленному типу int:
Если добавить в код проверку, что извлеченный символ строки действительно является цифрой, то программа станет более универсальной. С ее помощью можно будет считать не только сумму и произведение цифр целых чисел, но и вещественных, а также цифр, извлекаемых из произвольной строки.
Строковый метод isdigit() проверяет, состоит ли строка только из цифр. В нашем случае роль строки играет одиночный, извлеченный на текущей итерации цикла, символ.
Глубокое знание языка Python позволяет решить задачу более экзотическими способами:
Встроенная функция sum() считает сумму элементов переданного ей аргумента.
Сумма разрядных слагаемых
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Сумма разрядных слагаемых
Любое натуральное многозначное число можно представить в виде суммы разрядных слагаемых. Сумму разрядных слагаемых можно записать следующим образом:
35 = 3 десятка + 5 единиц = 3*10 = 30 + 5 = 35.
30 — разрядное слагаемое; 5 — разрядное слагаемое.
86 = 8 десятков + 6 единиц = 8*10 = 80 + 6 = 86
80 — разрядное слагаемое; 5 — разрядное слагаемое.
356 = 3 сотни + 5 десятков + 6 единиц = 3*100 + 5*10 + 6 = 300+50+6 = 356.
300, 50, 6 — разрядные слагаемые.
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Разряды и классы чисел
Чтобы без труда записывать числа в виде суммы разрядных слагаемых, нужно безошибочно определять класс и разряд числа.
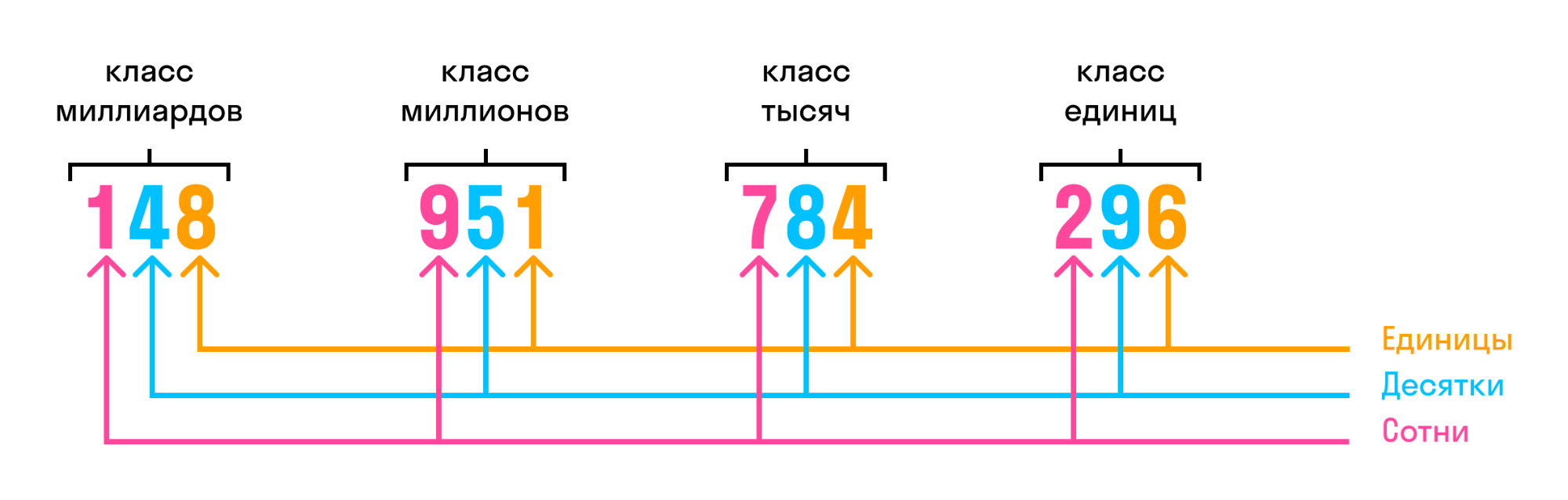
В многозначном числе цифры справа налево разбиваются на группы по три цифры. Такие группы называют классами.
Названия классов многозначных чисел:
Чтобы чтение многозначного числа не превращалось в головоломку, при записи лучше разграничивать число по классам. Вот так:
Читаться такое число будет слева направо: триста сорок пять миллиардов четыреста шестьдесят шесть миллионов сто двадцать девять тысяч триста пятьдесят.
Разряд — это место, которое занимает цифра в записи многозначного числа.
Разряды считаются справа налево. Первая цифра справа в записи числа относится к первому разряду.
Разрядные единицы — это единицы, десятки, сотни, тысячи, миллионы.
Все разрядные единицы, за исключением простых единиц, — составные единицы. Каждые десять единиц одного разряда составляют одну единицу следующего разряда.
Если составная единица больше другой единицы — она называется единицей высшего разряда. Если меньше, то единицей низшего разряда. Так, например, сотня — единица высшего разряда относительно десятка, но низшего разряда относительно тысячи.
Чтобы выяснить сколько всего в числе единиц определенного разряда, нужно мысленно вычеркнуть из числа все цифры низшего разряда.
Это значит, нужно выяснить, сколько сотен заключается в тысячах и в сотнях этого числа. 5689 — на третьем месте в классе единиц стоит цифра 6, значит в числе есть 6 сотен. Следующая влево цифра — 5 (тысячи). 1 тысяча = 10 сотен. 5 тысяч = 50 сотен. Всего в числе 56 сотен.
Если в разряде стоит цифра 0, то это означает отсутствие единиц, десятков, сотен и т.д., в зависимости от того, где именно содержится цифра.
Иногда бывает необходимо не только разложить число на разрядные слагаемые, но и определить количество единиц какого-то определенного разряда.
В такой ситуации можете выполнить подробный разбор числа.
Шесть миллионов пятьдесят семь тысяч триста восемьдесят шесть
6 057 386 = 6 * 1 000 000 + 0 * 100 000 + 5 * 10 000 + 7 * 1000 + 3 * 100 + 8 * 10 + 6 = 6 000 000 + 50 000 + 7 000 + 300 + 80 + 6.
Из чего состоит это число? Из:
Для того, чтобы алгоритм разложения числа на простые слагаемые был всегда под рукой, сохраняйте себе табличку с примером. В ней вы найдете вопросы, которые помогут разложите любое число.
Определите, сколько единиц в числе 5 068 252.
1. Определяем сколько всего единиц в числе.
2. Определяем количество десятков.
Записываем число без первого разряда (единицы).
3. Определяем количество сотен.
Записываем число без первого
и второго разрядов (десятки и сотни).
4. Определяем количество единиц тысяч.
Записываем число без первого, второго,
третьего разрядов (единицы, десятки, сотни).
5. Определяем количество десятков тысяч.
Записываем число без первого, второго, третьего,
четвертого разрядов (единицы, десятки, сотни, единицы тысяч).
6. Определяем количество сотен тысяч.
Записываем число без десятков тысяч, единиц тысяч,
сотен и единиц.
7. Определяем количество единиц миллионов.
Записываем число без сотен тысяч, десятков тысяч,
единиц тысяч, сотен, десятков, единиц.
Расписав таким образом число, мы выяснили, что в числе 5 068 252: 5 единиц класса миллионов (3 класс); 68 единиц класса тысяч (2 класс); 252 единицы класса единиц (1 класс).
Может показаться, что такой подробный разбор ни к чему, что и без того все понятно, но многоразрядные многозначные числа — коварны. Лучше хорошенько потренироваться, используя все вспомогательные материалы, как эта табличка, а потом уже раскладывать любое число за секунды и в уме.
Примеры
Внимательно просмотрите примеры и попробуйте самостоятельно представить числа в виде суммы разрядных слагаемых.
Представьте в виде суммы разрядных слагаемых:
Как видите, все довольно просто. Занятие весьма успокаивающее, медитативное. Приятно сесть после тяжелого дня и пораскладывать числа на разрядные слагаемые.
Если вдруг так вышло, что вы не расслабляетесь при виде цифр, то воспользуйтесь онлайн-калькулятором. В интернете таких калькуляторов немало, вот один из них.
Так вы сможете разложить на разрядные слагаемые любое, даже самое гигантское, число. Важно разобраться в разрядах и классах чисел, тогда вы точно ничего не перепутаете.
Использование функции СУММ для суммирования чисел в диапазоне
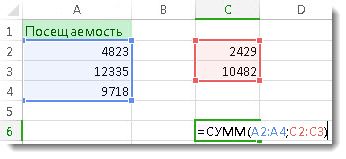
Для суммы чисел в диапазоне (группе ячеек) можно использовать простую формулу, но функцию СУММ проще использовать при работе с несколькими числами. Например, =СУММ(A2:A6) реже имеет ошибки при вводе, чем =A2+A3+A4+A5+A6.
Вот формула, использующая два диапазонаячеев: =СУММ(A2:A4;C2:C3) суммирует числа в диапазонах A2:A4 и C2:C3. Чтобы получить итоговую сумму в 39787, нажмите ввод.
Чтобы создать формулу:
Введите в ячейку =СУММ и открываю скобки (.
Чтобы ввести первый диапазон формул, который называется аргументом (частью данных, которую нужно выполнить), введите A2:A4 (или выберите ячейку A2 и перетащите ее через ячейку A6).
Введите запятую (,), чтобы отделить первый аргумент от следующего.
Введите второй аргумент C2:C3 (или перетащите его, чтобы выбрать ячейки).
Введите закрываюю скобки )и нажмите ввод.
Каждый аргумент может быть диапазоном, числом или ссылками на отдельные ячейки, разделенными запятой.
Совет: Если вам нужно свести столбцы или строки чисел рядом друг с другом, используйте авто сумму чисел.
Попробуйте попрактиковаться
Если вы хотите поиграть с образцом данных, воспользуйтесь некоторыми данными.
Чтобы узнать, как работает функция СУММ, скопируйте таблицу ниже в таблицу и вкопируйте ее в ячейку A1.
Прибавляет 5, 15 и 1. Текстовое значение «5» сначала переводится в число, а логическое значение ИСТИНА — в число 1.
Суммы значений в ячейках A2-A4.
С суммой значений в ячейках A2–A4, а затем к результату прибавляет 15.
Суммы значений в ячейках A5 и A6, а затем 2 к результату. Так как не числовые значения в ссылках не переводятся, значение в ячейке A5 (‘5) и значение в ячейке A6 (ИСТИНА) будут рассматриваться как текст, поэтому значения в этих ячейках игнорируются.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.