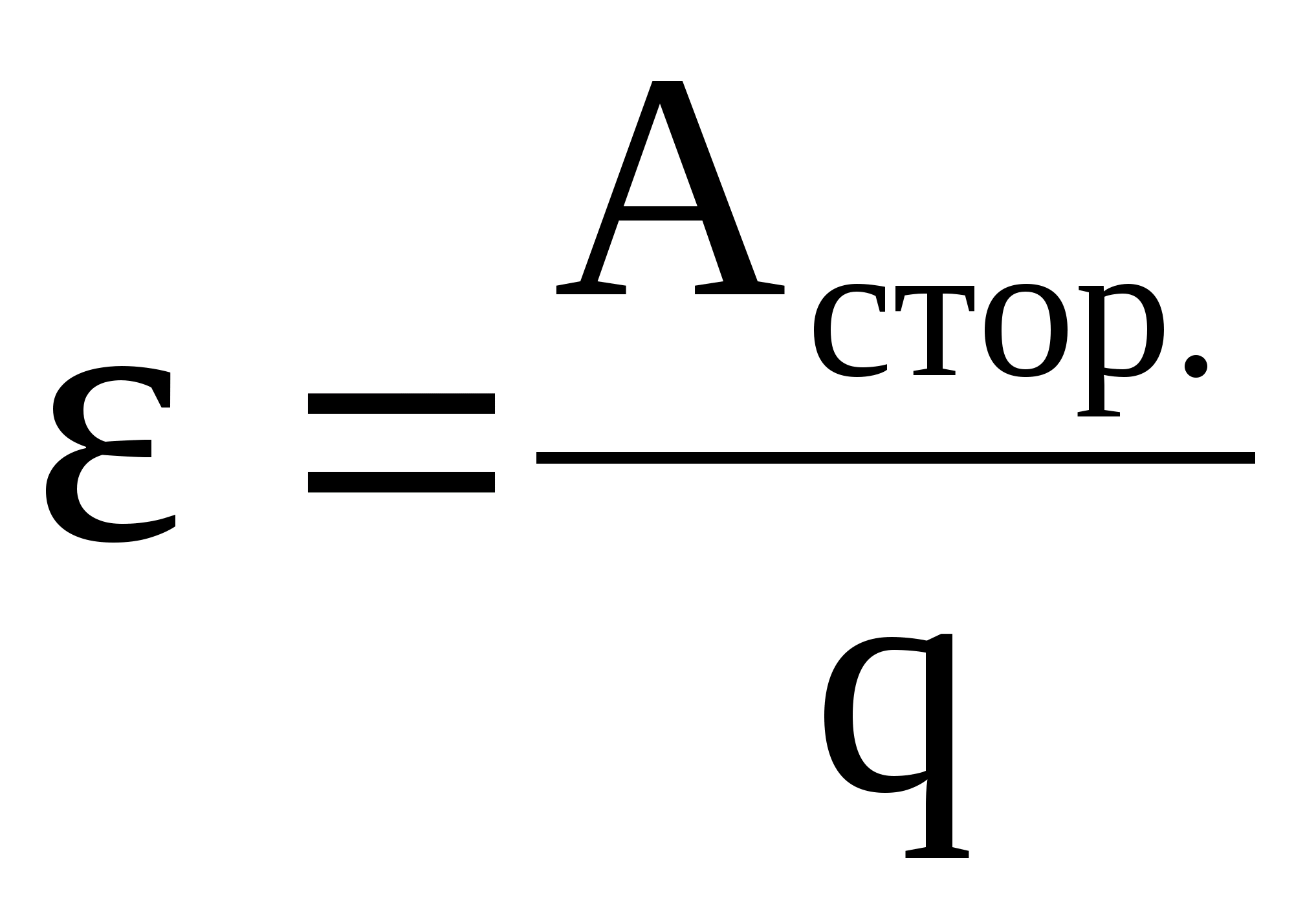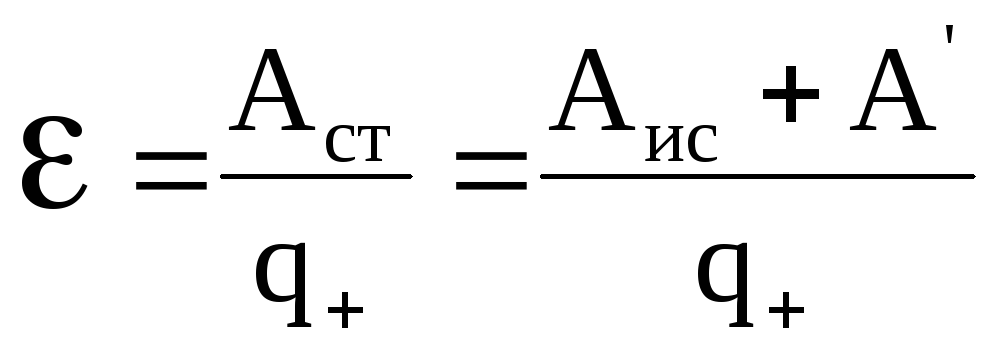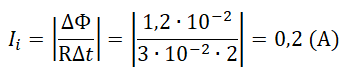Что такое электродвижущая сила (ЭДС) и как ее рассчитать
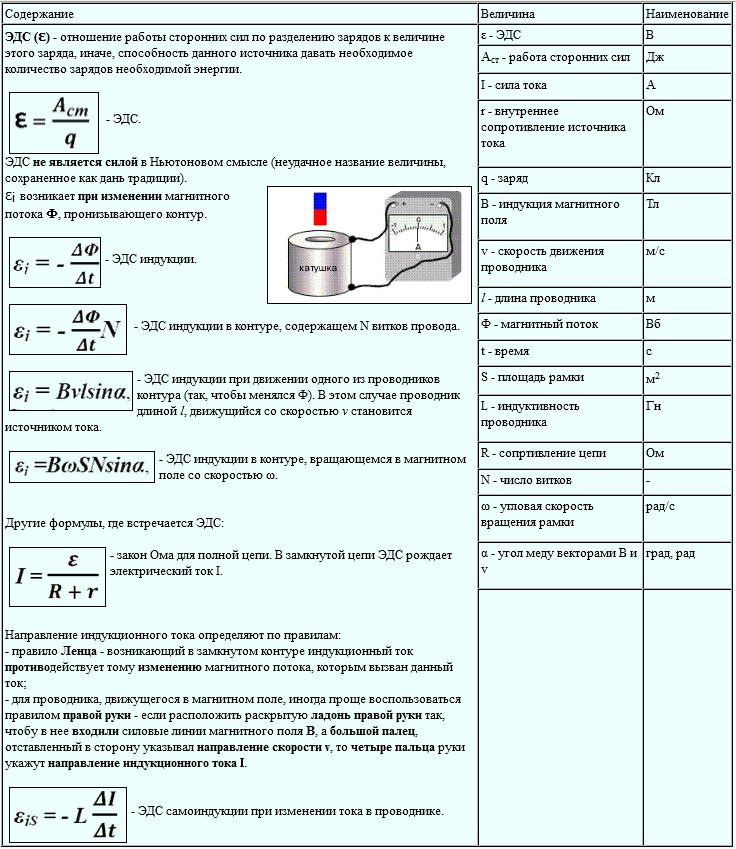
Электродвижущая сила или сокращено ЭДС – это способность источника тока ил по-другому питающий элемент, создавать в электрической цепи разность потенциалов. Элементами питания являются аккумуляторы или батареи. Это скалярная физическая величина, равная работе сторонних сил для перемещения одного заряда с положительной величиной. В данной статье будут рассмотрены теоритические вопросы ЭДС, как она образуется, а также для чего она может быть использована на практике и где используются, а главное как рассчитать ее.
Что такое ЭДС: объяснение простыми словами
В физике она соответствует электродвижущей силе, создаваемой на концах электрической термопары, например. Чтобы объяснить суть ЭДС простыми словами – потребуется рассмотреть каждый из вариантов ее трактовки. Прежде чем перейти к основной части статьи отметим, что ЭДС и напряжение очень близкие по смыслу понятия, но всё же несколько отличаются. Если сказать кратко, то ЭДС — на источнике питания без нагрузки, а когда к нему подключают нагрузку — это уже напряжение. Потому что количество вольт на ИП под нагрузкой почти всегда несколько меньше, чем без неё. Это связано с наличием внутреннего сопротивления таких источников питания, как трансформаторы и гальванические элементы.
Сторонние силы приводят в движение заряженные частицы внутри источников тока: генераторов, гальванических элементов, аккумуляторов и т. д. Происхождение сторонних сил может быть различным. В генераторах сторонние силы — это силы со стороны вихревого электрического поля, возникающего при изменении магнитного поля со временем, или Лоренца сила, действующая со стороны магнитного поля на электроны в движущемся проводнике; в гальванических элементах и аккумуляторах — это химические силы и т. д. Эдс определяет силу тока в цепи при заданном её сопротивлении (см. Ома закон). Измеряется эдс, как и напряжение, в вольтах.
Природа ЭДС
Причина возникновения ЭДС в разных источниках тока разная. По природе возникновения различают следующие типы:
Электромагнитная индукция (самоиндукция)
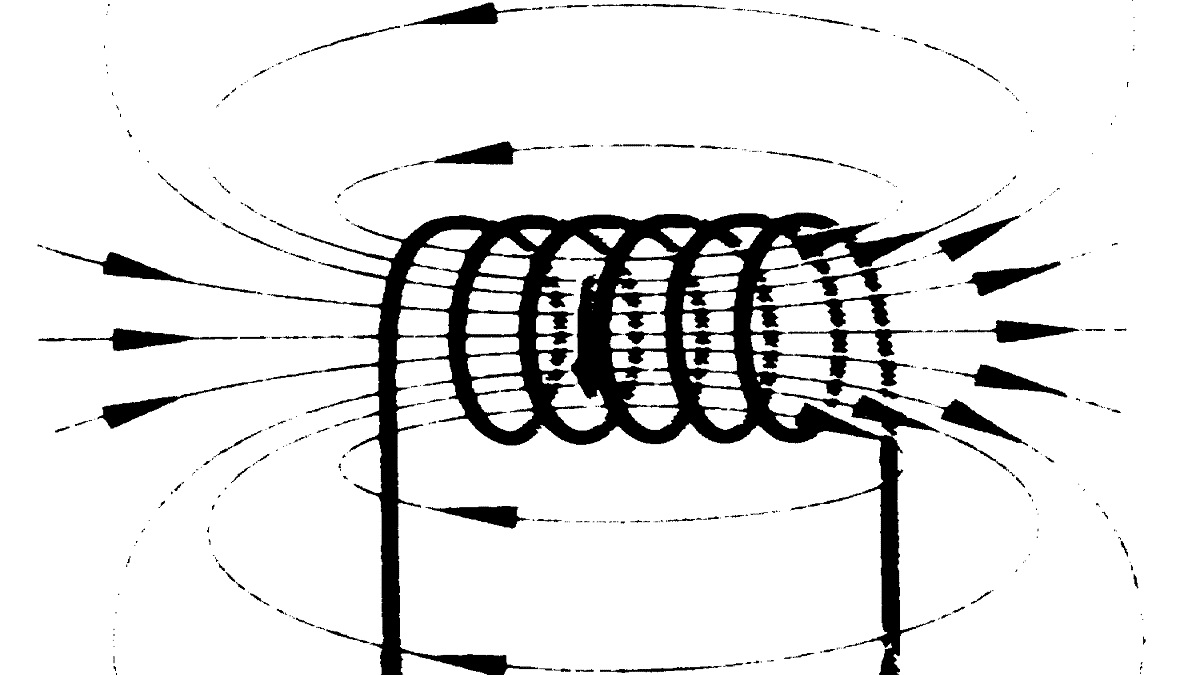
Начнем с электромагнитной индукции. Это явление описывает закон электромагнитной индукции Фарадея. Физический смысл этого явления состоит в способности электромагнитного поля наводить ЭДС в находящемся рядом проводнике. При этом или поле должно изменяться, например, по величине и направлению векторов, или перемещаться относительно проводника, или должен двигаться проводник относительно этого поля. На концах проводника в этом случае возникает разность потенциалов.
Опыт демонстрирует появление ЭДС в катушке при воздействии изменяющегося магнитного поля постоянного магнита. Есть и другое похожее по смыслу явление — взаимоиндукция. Оно заключается в том, что изменение направления и силы тока одной катушки индуцирует ЭДС на выводах расположенной рядом катушки, широко применяется в различных областях техники, включая электрику и электронику. Оно лежит в основе работы трансформаторов, где магнитный поток одной обмотки наводит ток и напряжение во второй.
В электрике физический эффект под названием ЭДС используется при изготовлении специальных преобразователей переменного тока, обеспечивающих получение нужных значений действующих величин (тока и напряжения). Благодаря явлениям индукции и самоиндукции инженерам удалось разработать множество электротехнических устройств: от обычной катушки индуктивности (дросселя) и вплоть до трансформатора. Понятие взаимоиндукции касается только переменного тока, при протекании которого в контуре или проводнике меняется магнитный поток.
ЭДС в быту и единицы измерения
Другие примеры встречаются в практической жизни любого рядового человека. Под эту категорию попадают такие привычные вещи, как малогабаритные батарейки, а также другие миниатюрные элементы питания. В этом случае рабочая ЭДС формируется за счет химических процессов, протекающих внутри источников постоянного напряжения. Когда оно возникает на клеммах (полюсах) батареи вследствие внутренних изменений – элемент полностью готов к работе. Со временем величина ЭДС несколько снижается, а внутреннее сопротивление заметно возрастает.
В результате если вы измеряете напряжение на не подключенной ни к чему пальчиковой батарейке вы видите нормальные для неё 1.5В (или около того), но когда к батарейке подключается нагрузка, допустим, вы установили её в какой-то прибор — он не работает. Почему? Потому что если предположить, что у вольтметра внутреннее сопротивление во много раз выше, чем внутреннее сопротивлении батарейки — то вы измеряли её ЭДС. Когда батарейка начала отдавать ток в нагрузке на её выводах стало не 1.5В, а, допустим, 1.2В — прибору недостаточно ни напряжения, ни тока для нормальной работы.
Как раз вот эти 0.3 В и упали на внутреннем сопротивлении гальванического элемента. Если батарейка совсем старая и её электроды разрушены, то на клеммах батареи может не быть вообще никакой электродвижущей силы или напряжения — т.е. ноль. Совсем небольшая по величине электродвижущая сила наводится и в рамках антенны приемника, которая усиливается затем специальными каскадами, и мы получаем наш телевизионный, радио и даже Wi-Fi сигнал.
Как образуется ЭДС
Идеальный источник ЭДС – генератор, внутреннее сопротивление которого равно нулю, а напряжение на его зажимах не зависит от нагрузки. Мощность идеального источника ЭДС бесконечна. Реальный источник ЭДС, в отличие от идеального, содержит внутреннее сопротивление Ri и его напряжение зависит от нагрузки (рис. 1., б), а мощность источника конечна. Электрическая схема реального генератора ЭДС представляет собой последовательное соединение идеального генератора ЭДС Е и его внутреннего сопротивления Ri.
На практике для того чтобы приблизить режим работы реального генератора ЭДС к режиму работы идеального, внутреннее сопротивление реального генератора Ri стараются делать как можно меньше, а сопротивление нагрузки Rн необходимо подключать величиной не менее чем в 10 раз большей величины внутреннего сопротивления генератора, т.е. необходимо выполнять условие: Rн >> Ri
Для того чтобы выходное напряжение реального генератора ЭДС не зависело от нагрузки, его стабилизируют применением специальных электронных схем стабилизации напряжения. Поскольку внутреннее сопротивление реального генератора ЭДС не может быть выполнено бесконечно малым, его минимизируют и выполняют стандартным для возможности согласованного подключения к нему потребителей энергии. В радиотехнике величины стандартного выходного сопротивления генераторов ЭДС составляют 50 Ом (промышленный стандарт) и 75 Ом (бытовой стандарт).
Например, все телевизионные приемники имеют входное сопротивление 75 Ом и подключены к антеннам коаксиальным кабелем именно такого волнового сопротивления. Для приближения к идеальным генераторам ЭДС источники питающего напряжения, используемые во всей промышленной и бытовой радиоэлектронной аппаратуре, выполняют с применением специальных электронных схем стабилизации выходного напряжения, которые позволяют выдерживать практически неизменное выходное напряжение источника питания в заданном диапазоне токов, потребляемых от источника ЭДС (иногда его называют источником напряжения).
На электрических схемах источники ЭДС изображаются так: Е — источник постоянной ЭДС, е(t) – источник гармонической (переменной) ЭДС в форме функции времени. Электродвижущая сила Е батареи последовательно соединенных одинаковых элементов равна электродвижущей силе одного элемента Е, умноженной на число элементов n батареи: Е = nЕ.
Электродвижущая сила (ЭДС) источника энергии
Для поддержания электрического тока в проводнике требуется внешний источник энергии, создающий все время разность потенциалов между концами этого проводника. Такие источники энергии получили название источников электрической энергии (или источников тока). Источники электрической энергии обладают определенной электродвижущей силой (сокращенно ЭДС), которая создает и длительное время поддерживает разность потенциалов между концами проводника.
Как написать уравнение эдс
Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.
В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.
 , | (1) |
Величина, обратная периоду, есть частота, измеряемая в герцах (Гц):
 , | (2) |
Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:
u – мгновенное значение напряжения 
;
— амплитуда тока;
— амплитуда напряжения;
— амплитуда ЭДС.
Действующее значение переменного тока
Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:
 , | (3) |
Аналогично определяются действующие значения ЭДС и напряжения.
Синусоидально изменяющийся ток
Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.
Изображение синусоидальных ЭДС, напряжений
и токов на плоскости декартовых координат
Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.
Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е1 и е2 соответствуют уравнения:
Значения аргументов синусоидальных функций 
и 
называются фазами синусоид, а значение фазы в начальный момент времени ( t =0): 
и 
— начальной фазой ( 
).
При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз.
Для синусоидальных ЭДС е1 и е2 угол сдвига фаз:
Векторное изображение синусоидально
изменяющихся величин
Пусть, например, в точке разветвления цепи (рис. 5) общий ток 
равен сумме токов 
и 
двух ветвей:
.
Каждый из этих токов синусоидален и может быть представлен уравнением
и 
.
Результирующий ток также будет синусоидален:
.
Определение амплитуды 
и начальной фазы 
этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы.
Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:
Представление синусоидальных ЭДС, напряжений
и токов комплексными числами
Геометрические операции с векторами можно заменить алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов.
Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в :
показательной 
тригонометрической 
или
Фазовый угол 
определяется по проекциям вектора на оси “+1” и “+j” системы координат, как
В соответствии с тригонометрической формой записи мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:
 , | (4) |
Комплексное число 
удобно представить в виде произведения двух комплексных чисел:
 , | (5) |
Параметр 
является оператором поворота вектора на угол w t относительно начального положения вектора.
Следовательно, мгновенное значение синусоидальной величины равно мнимой части без знака “j” произведения комплекса амплитуды 
и оператора поворота :
Переход от одной формы записи синусоидальной величины к другой осуществляется с помощью формулы Эйлера:
 , | (6) |
Если, например, комплексная амплитуда напряжения задана в виде комплексного числа в алгебраической форме:
Тогда мгновенное значение напряжения:
 , | (7) |
а при 
(третий квадрант)
 | (8) |
 | (9) |
Следует указать, что при сложении и вычитании комплексов следует пользоваться алгебраической формой их записи, а при умножении и делении удобна показательная форма.
Итак, применение комплексных чисел позволяет перейти от геометрических операций над векторами к алгебраическим над комплексами. Так при определении комплексной амплитуды результирующего тока по рис. 5 получим:
где 
;
Действующее значение синусоидальных ЭДС, напряжений и токов
В соответствии с выражением (3) для действующего значения синусоидального тока запишем:
Аналогичный результат можно получить для синусоидальных ЭДС и напряжений. Таким образом, действующие значения синусоидальных тока, ЭДС и напряжения меньше своих амплитудных значений в 
раз:
 . | (10) |
Поскольку, как будет показано далее, энергетический расчет цепей переменного тока обычно проводится с использованием действующих значений величин, по аналогии с предыдущим введем понятие комплекса действующего значения
2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
1. Какой практический смысл имеет изображение синусоидальных величин с помощью векторов?
2. Какой практический смысл имеет представление синусоидальных величин с использованием комплексных чисел?
3. В чем заключаются преимущества изображения синусоидальных величин с помощью комплексов по сравнению с их векторным представлением?
4. Для заданных синусоидальных функций ЭДС и тока 
записать соответствующие им комплексы амплитуд и действующих значений, а также комплексы мгновенных значений.
Закон электромагнитной индукции
теория по физике ? магнетизм
Магнитный поток наглядно истолковывается как число линий магнитной индукции, пронизывающих поверхность площадью S. Поэтому скорость изменения этого числа есть не что иное, как скорость изменения магнитного потока.
Сила индукционного тока пропорциональная скорости изменения магнитного потока через поверхность, ограниченную контуром:
Согласно закону Ома для замкнутой цепи:
Сопротивление проводника не зависит от изменения магнитного потока. Следовательно, сила индукционного тока пропорциональна скорости изменения магнитного потока только потому, что ЭДС индукции тоже пропорциональна этой скорости изменения потока.
Закон электромагнитной индукции
ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром.
Закон электромагнитной индукции формулируется именно для ЭДС, а не для силы тока. При такой формулировке закон выражает сущность явления, не зависящую от свойств проводников, в которых возникает индукционный ток.
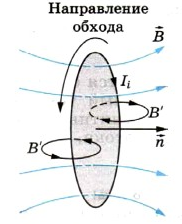
Определение знака ЭДС индукции
На рисунке изображен замкнутый контур. Будем считать положительным направление обхода контура против часовой стрелки. Нормаль → n к контуру образует правый винт с направлением обхода.
Пример №1. Магнитный поток через контур проводника сопротивлением 3∙10 –2 Ом за 2 с изменился на 1,2∙10 –2 Вб. Найдите силу тока в проводнике, если изменение потока происходило равномерно.
ЭДС индукции в движущихся проводниках
Электроны в неподвижном проводнике приводятся в движение электрическим полем, и это поле порождается переменным магнитным полем. Следовательно, изменяясь во времени, магнитное поле порождает электрическое поле. Но если проводник движется в постоянном во времени магнитном поле, то ЭДС индукции в проводнике обусловлена не вихревым электрическим полем, которое в этом случае не может возникнуть, а другой причиной.
При движении проводника его свободные заряды движутся вместе с ним. Поэтому на заряды со стороны магнитного поля действует сила Лоренца. Она и вызывает перемещение зарядов внутри проводника. ЭДС индукции, следовательно, имеет магнитное происхождение.
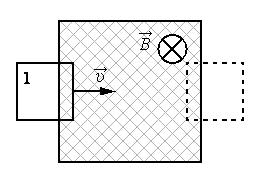
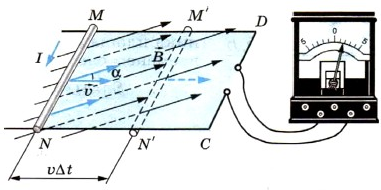
Вычислим ЭДС индукции, возникающую в проводнике, движущемся в однородном магнитном поле (см. рисунок). Пусть сторона контура MN длиной l скользит с постоянной скоростью → v вдоль сторон NC и MD, оставаясь все это время параллельной стороне CD. Вектор магнитной индукции → B однородного поля перпендикулярен проводнику и составляет угол α с направлением его скорости.
Сила, с которой магнитное поле действует на движущуюся заряженную частицу, равна по модулю:
Направлена эта сила вдоль проводника MN. Работа силы Лоренца на пути l положительна и составляет:
Формула выше определяет неполную работу силы Лоренца. Кроме силы Лоренца имеется составляющая силы Лоренца, направленная против скорости проводника → v . Такая составляющая тормозит проводник и совершает отрицательную работу. В результате полная работа силы Лоренца оказывается равной нулю.
Электродвижущая сила индукции в проводнике MN равна по определению отношению работы по перемещению заряда q к этому заряду:
Эта формула справедлива для любого проводника длиной l, движущегося со скоростью → v в однородном магнитном поле.
В других проводниках контура ЭДС равна нулю, так как проводники неподвижны. Следовательно, ЭДС во всем контуре MNCD равна ε i и остается неизменной, если скорость движения → v постоянна. Электрический ток при этом будет увеличиваться, так как при смещении проводника MN вправо уменьшается общее сопротивление контура.
С другой стороны, ЭДС индукции можно вычислить с помощью закона электромагнитной индукции. Магнитный поток через контур MNCD равен:
угол 90 ° − α представляет собой угол между векторами → B и нормалью → n к поверхности контура, а S — площадь контура MNCD. Если считать, что в начальный момент времени t=0 проводник MN находится на расстоянии NC от проводника CD, то при перемещении проводника площадь S изменяется со временем следующим образом:
Пример №2. Проводник длиной 50 см движется в однородном магнитном поле со скоростью 4 м/с перпендикулярно силовым линиям. Найдите разность потенциалов, возникающую на концах проводника, если вектор магнитной индукции 8 мТл.
Так как проводник движется перпендикулярно силовым линиям, то угол α равен 90 градусам, а синус прямого угла равен единице. Поэтому:
В заштрихованной области на рисунке действует однородное магнитное поле, направленное перпендикулярно плоскости рисунка, В = 0,1 Тл. Проволочную квадратную рамку сопротивлением R=10Ом и стороной l=10см перемещают в плоскости рисунка поступательно со скоростью υ=1м/с. Чему равен индукционный ток в рамке в состоянии 1?